题目内容
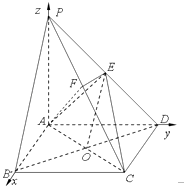
【题目】如图,四棱锥P﹣ABCD的底面ABCD为矩形,PA⊥平面ABCD,点E是棱PD的中点,点F是PC的中点F. 
(1)证明:PB∥平面AEC;
(2)若ABCD为正方形,探究在什么条件下,二面角C﹣AF﹣D大小为60°?
【答案】
(1)证明:连接BD,设AC∩BD=O,连结OE,
∵四边形ABCD为矩形,
∴O是BD的中点,
∵点E是棱PD的中点,
∴PB∥EO,
又PB平面AEC,EO平面AEC,
∴PB∥平面AEC.
(2)解:由题意知AD,AB,AP两两垂直,建立如图所示空间直角坐标系A﹣xyz,
设AB=2a,AD=2b,AP=2c,
则A(0,0,0),B(2a,0,0),C(2a,2b,0),D(0,2b,0),P(0,0,2c).
设AC∩BD=O,连结OE,则O(a,b,0),E(0,b,c).
因为 ![]() ,
, ![]() ,
,
所以 ![]() ,所以
,所以 ![]() ∥
∥ ![]() ,a=b,A(0,0,0),B(2a,0,0),
,a=b,A(0,0,0),B(2a,0,0),
C(2a,2a,0),D(0,2a,0),P(0,0,2c),E(0,a,c),F(a,a,c),
因为z轴平面CAF,所以设平面CAF的一个法向量为 ![]() =(x,1,0),
=(x,1,0),
而 ![]() ,所以
,所以 ![]() =2ax+2a=0,得x=﹣1,所以
=2ax+2a=0,得x=﹣1,所以 ![]() =(﹣1,1,0).
=(﹣1,1,0).
因为y轴平面DAF,所以设平面DAF的一个法向量为 ![]() =(1,0,z),
=(1,0,z),
而 ![]() ,所以
,所以 ![]() =a+cz=0,得
=a+cz=0,得 ![]() ,
,
所以 ![]() =(1,0,﹣
=(1,0,﹣ ![]() )∥
)∥ ![]() =(c,0,﹣a).
=(c,0,﹣a).
cos60°= ![]() =
= ![]() ,得a=c.
,得a=c.
即当AP等于正方形ABCD的边长时,二面角C﹣AF﹣D的大小为60°.
【解析】(1)连接BD,设AC∩BD=O,连结OE,则PB∥EO,由此能证明PB∥平面AEC.(2)由题意知AD,AB,AP两两垂直,建立空间直角坐标系A﹣xyz,利用向量法能求出当AP等于正方形ABCD的边长时,二面角C﹣AF﹣D的大小为60°.
【考点精析】掌握直线与平面平行的判定是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
