题目内容
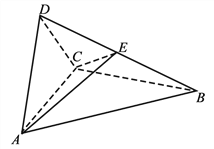
【题目】如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D. 
(1)求证:CE2=CDCB.
(2)若AB=2,BC= ![]() ,求CE与CD的长.
,求CE与CD的长.
【答案】
(1)证明:如图示:

连接BE,
∵BC为⊙O的切线∴∠ABC=90°,
∵AB为⊙O的直径∴∠AEB=90°,
∴∠DBE+∠OBE=90°,∠AEO+∠OEB=90°,
∵OB=OE,∴∠OBE=∠OEB∴∠DBE=∠AEO,
∵∠AEO=∠CED∴∠CED=∠CBE,
∵∠C=∠C∴△CED∽△CBE,
∴ ![]() =
= ![]() ,∴CE2=CDCB;
,∴CE2=CDCB;
(2)解:∵OB=1,BC= ![]() ,∴OC=
,∴OC= ![]() ,
,
∴CE=OC﹣OE= ![]() ,
,
由(Ⅰ)得:CE2=CDCB,
∴ ![]() =
= ![]() CD,
CD,
∴CD= ![]() .
.
【解析】(1)要证CE2=CDCB,结合题意,只需证明△CED∽△CBE即可,故连接BE,利用弦切角的知识即可得证;(2)在Rt三△OBC中,利用勾股定理即可得出CE的长,由(1)知,CE2=CDCB,代入CE即可得出CD的长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对![]() 名小学六年级学生进行了问卷调查,并得到如下列联表.平均每天喝
名小学六年级学生进行了问卷调查,并得到如下列联表.平均每天喝![]() 以上为“常喝”,体重超过
以上为“常喝”,体重超过![]() 为“肥胖”.
为“肥胖”.
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
合计 | 30 |
已知在全部![]() 人中随机抽取
人中随机抽取![]() 人,抽到肥胖的学生的概率为
人,抽到肥胖的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有![]() 的把握认为肥胖与常喝碳酸饮料有关?请说明你的理由;
的把握认为肥胖与常喝碳酸饮料有关?请说明你的理由;
(3)已知常喝碳酸饮料且肥胖的学生中恰有2名女生,现从常喝碳酸饮料且肥胖的学生中随机抽取2人参加一个有关健康饮食的电视节目,求恰好抽到一名男生和一名女生的概率.
附:![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|