题目内容
【题目】已知在![]() 上的函数
上的函数![]() ,
, ![]() ,
,
其中![]() ,设两曲线
,设两曲线![]() 有公共点,且在公共点处的切线相同.
有公共点,且在公共点处的切线相同.
(Ⅰ)若![]() ,求
,求![]() 的值;
的值;
(Ⅱ)用![]() 表示
表示![]() ,并求
,并求![]() 的最大值。
的最大值。
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() ,
, ![]() 的最大值为
的最大值为![]() .
.
【解析】试题分析:(1)设y=f(x)与y=g(x)(x>0)在公共点(x0,y0)处的切线相同,先利用导数求出在切点处的导函数值,再结合导数的几何意义即可求出切线的斜率.最后利用两直线重合列出等式即可求得b值;
(2)利用(1)类似的方法,利用a的表达式来表示b,然后利用导数来研究b的最大值,研究此函数的最值问题,先求出函数的极值,结合函数的单调性,最后确定出最大值与最小值即得.
试题解析:
(Ⅰ)设y=f(x)与y=g(x)(x>0)在公共点![]() 处的切线相同
处的切线相同![]() ,由题意知
,由题意知![]() ,
,
∴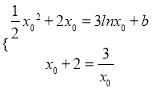 由
由![]() 得,
得, ![]() 或
或![]() (舍去),即有
(舍去),即有![]()
(Ⅱ)设y=f(x)与y=g(x) (x>0)在公共点![]() 处的切线相同
处的切线相同![]() ,由题意知
,由题意知![]() ,
, 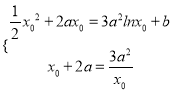
∴![]() 由得,
由得, ![]() 或
或![]() (舍去)
(舍去)
即有![]() , 令
, 令![]() (t>0),
(t>0),
则![]() ,于是当2t(1-3lnt)>0,即
,于是当2t(1-3lnt)>0,即![]() 时,
时, ![]() ;
;
当2t(1-3lnt)<0,即![]() 时,
时, ![]() ,故h(t)在
,故h(t)在![]() 的最大值为
的最大值为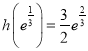 ,
,
故![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
相关题目