题目内容
已知函数y=f(x),对任意x,y∈R,都有f(x+y)=f(x)+f(y)+m,则函数g(x)=f(x)+m+3ln
,x∈[-1,1]的最大值与最小值之和是______.
| e |
∵函数y=f(x),对任意x,y∈R,都有f(x+y)=f(x)+f(y)+m,
∴令x=y=0时,f(0)=f(0)+f(0)+m,
∴f(0)=-m,
令y=-x时,f(0)=f(x)+f(-x)+m,
∴f(x)+f(-x)=-2m,
令h(x)=f(x)+m,则h(x)+h(-x)=0即h(x)为奇函数,
奇函数的图象关于原点对称,它的最大值与最小值互为相反数,
设h(x)在[-1,1]的最大值为M,则h(x)在[-1,1]的最小值为-M,
∴函数g(x)在[-1,1]的最大值为3ln
+M,则g(x)在[-1,1]的最小值为3ln
-M,
∴函g(x)=f(x)+m+3ln
在[-1,1]的最大值与最小值之和为6ln
=3.
故答案为:3.
∴令x=y=0时,f(0)=f(0)+f(0)+m,
∴f(0)=-m,
令y=-x时,f(0)=f(x)+f(-x)+m,
∴f(x)+f(-x)=-2m,
令h(x)=f(x)+m,则h(x)+h(-x)=0即h(x)为奇函数,
奇函数的图象关于原点对称,它的最大值与最小值互为相反数,
设h(x)在[-1,1]的最大值为M,则h(x)在[-1,1]的最小值为-M,
∴函数g(x)在[-1,1]的最大值为3ln
| e |
| e |
∴函g(x)=f(x)+m+3ln
| e |
| e |
故答案为:3.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
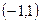 上的函数
上的函数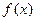 满足:①对任意的
满足:①对任意的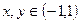 ,都有
,都有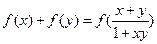 ;②当
;②当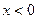 时,
时,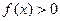
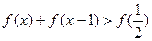
 ,+∞
,+∞

 ,+∞
,+∞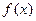 满足条件:
满足条件: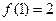 ,
,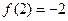 ,
,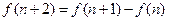 ,则
,则 的值为( )
的值为( )