题目内容
函数f(x)的定义域为R,且x≠1,已知f(x+1)为奇函数,当x<1时,f(x)=2x2–x+1,那么当x>1时,f(x)的递减区间是( )
A.[ ,+∞ ,+∞ | B.(1,  | C.[ ,+∞ ,+∞ | D. (1, ] ] |
C
由题意可得f(–x+1)=–f(x+1).令t=–x+1,则x=1–t,
故f(t)=–f(2–t),即f(x)=–f(2–x).
当x>1,2–x<1,于是有f(x)=–f(2–x)=–2(x–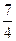 )2–
)2–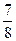 ,其递减区间为[
,其递减区间为[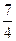 ,+∞).
,+∞).
故f(t)=–f(2–t),即f(x)=–f(2–x).
当x>1,2–x<1,于是有f(x)=–f(2–x)=–2(x–
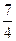 )2–
)2–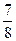 ,其递减区间为[
,其递减区间为[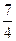 ,+∞).
,+∞). 
练习册系列答案
相关题目
 的定义域是R,对于任意实数
的定义域是R,对于任意实数 ,恒有
,恒有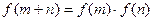 ,且当
,且当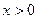 时,
时,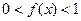 .
.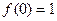 ,且当
,且当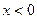 时,有
时,有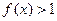 ;
;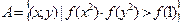 ,集合
,集合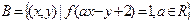 ,若
,若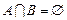 ,求
,求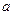 的取值范围.
的取值范围.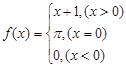 ,则
,则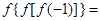 ( ).
( ).



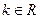 ,函数
,函数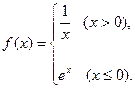 ,
,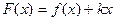 ,
,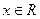 .
.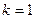 时,求
时,求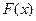 的值域;
的值域;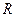 上的函数
上的函数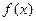 满足
满足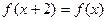 ,当
,当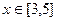 时
时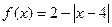 ,则
,则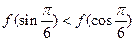
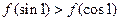
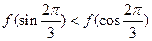
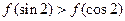
 ,则
,则 。
。 ,则
,则