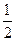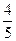题目内容
已知:函数f(x)对一切实数x,y都有f(x+y)-f(y)=x(x+2y+1)成立,且f(1)=0.
(1)求f(0)的值.
(2)求f(x)的解析式.
(3)已知a∈R,设P:当0<x<
时,不等式f(x)+3<2x+a恒成立;Q:当x∈[-2,2]时,g(x)=f(x)-ax是单调函数.如果满足P成立的a的集合记为A,满足Q成立的a的集合记为B,求A∩CRB(R为全集).
(1)求f(0)的值.
(2)求f(x)的解析式.
(3)已知a∈R,设P:当0<x<
| 1 |
| 2 |
(1)令x=-1,y=1,则由已知f(0)-f(1)=-1(-1+2+1)
∴f(0)=-2
(2)令y=0,则f(x)-f(0)=x(x+1)
又∵f(0)=-2
∴f(x)=x2+x-2
(3)不等式f(x)+3<2x+a即x2+x-2+3<2x+a
也就是x2-x+1<a.由于当0<x<
时,
<x2-x+1<1,又x2-x+1=(x-
)2+
<a恒成立,
故A={a|a≥1},g(x)=x2+x-2-ax=x2+(1-a)x-2 对称轴x=
,
又g(x)在[-2,2]上是单调函数,故有
≤-2,或
≥2,
∴B={a|a≤-3,或a≥5},CRB={a|-3<a<5}
∴A∩CRB={a|1≤a<5}.
∴f(0)=-2
(2)令y=0,则f(x)-f(0)=x(x+1)
又∵f(0)=-2
∴f(x)=x2+x-2
(3)不等式f(x)+3<2x+a即x2+x-2+3<2x+a
也就是x2-x+1<a.由于当0<x<
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
故A={a|a≥1},g(x)=x2+x-2-ax=x2+(1-a)x-2 对称轴x=
| a-1 |
| 2 |
又g(x)在[-2,2]上是单调函数,故有
| a-1 |
| 2 |
| a-1 |
| 2 |
∴B={a|a≤-3,或a≥5},CRB={a|-3<a<5}
∴A∩CRB={a|1≤a<5}.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 的定义域是R,对于任意实数
的定义域是R,对于任意实数 ,恒有
,恒有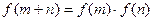 ,且当
,且当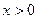 时,
时,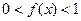 .
.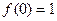 ,且当
,且当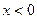 时,有
时,有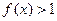 ;
;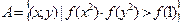 ,集合
,集合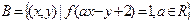 ,若
,若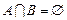 ,求
,求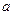 的取值范围.
的取值范围.
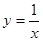 (x>0)图像上一动点,若点P,A之间的最短距离为
(x>0)图像上一动点,若点P,A之间的最短距离为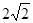 ,则满足条件的实数a所有值为_________.
,则满足条件的实数a所有值为_________.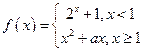 ,若
,若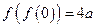 ,则实数
,则实数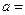 ( )
( )