题目内容
定义在区间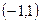 上的函数
上的函数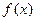 满足:①对任意的
满足:①对任意的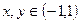 ,都有
,都有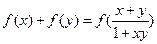 ;②当
;②当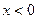 时,
时,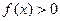
(1)求证f (x)为奇函数;(2)试解不等式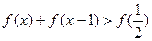
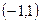 上的函数
上的函数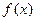 满足:①对任意的
满足:①对任意的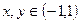 ,都有
,都有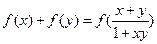 ;②当
;②当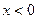 时,
时,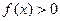
(1)求证f (x)为奇函数;(2)试解不等式
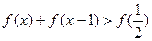
(1)证明见解析。
(2)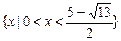
(2)
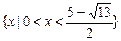
(1)解:令x = y = 0,则
f (0) + f (0) =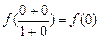
∴f (0) = 0
令x∈(-1, 1) ∴-x∈(-1, 1)
∴f (x) + f (-x) = f ( ) = f (0) = 0
) = f (0) = 0
∴f (-x) =-f (x)
∴f (x) 在(-1,1)上为奇函数
(2)解:令-1< x1 < x2 < 1
则f (x1) -f (x2) = f (x1) + f (-x2) =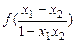
∵x1-x2 < 0,1-x1x2 > 0
∴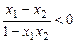 ∴
∴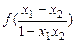 > 0
> 0
∴f (x1) > f (x2) ∴f (x) 在(-1,1)上为减函数
又f (x) + f (x-1) >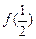

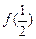
∴不等式化为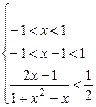
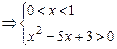
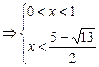 或
或

∴不等式的解集为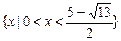
f (0) + f (0) =
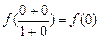
∴f (0) = 0
令x∈(-1, 1) ∴-x∈(-1, 1)
∴f (x) + f (-x) = f (
 ) = f (0) = 0
) = f (0) = 0∴f (-x) =-f (x)
∴f (x) 在(-1,1)上为奇函数
(2)解:令-1< x1 < x2 < 1
则f (x1) -f (x2) = f (x1) + f (-x2) =
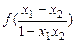
∵x1-x2 < 0,1-x1x2 > 0
∴
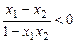 ∴
∴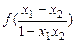 > 0
> 0∴f (x1) > f (x2) ∴f (x) 在(-1,1)上为减函数
又f (x) + f (x-1) >
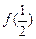

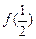
∴不等式化为
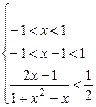
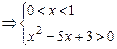
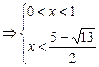 或
或

∴不等式的解集为
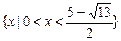

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
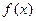 的定义域是R,对于任意实数
的定义域是R,对于任意实数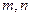 ,恒有
,恒有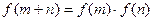 ,且当
,且当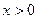 时,
时,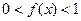 .
.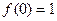 ,且当
,且当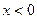 时,有
时,有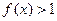 ;
;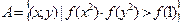 ,集合
,集合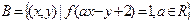 ,若
,若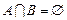 ,求
,求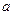 的取值范围.
的取值范围.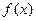 是定义在
是定义在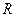 上的奇函数,当
上的奇函数,当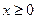 时,
时,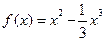 , (1)求函数
, (1)求函数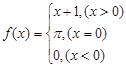 ,则
,则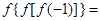 ( ).
( ).



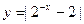 的单调增区间为
的单调增区间为  .
.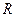 上的函数
上的函数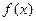 满足
满足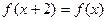 ,当
,当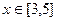 时
时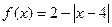 ,则
,则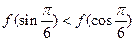
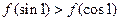
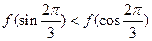
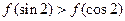
 对于一切实数
对于一切实数 均有
均有 成立,且
成立,且 ,则当
,则当 时,不等式
时,不等式 恒成立时,实数
恒成立时,实数 的取值范围是 ▲ .
的取值范围是 ▲ .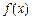 满足
满足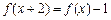 ,则
,则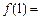 ( )
( )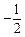 D.
D.