题目内容
若f(x)是定义在(0,+∞)上的增函数,且对一切x,y>0满足f(
)=f(x)-f(y).
(1)求f(1)的值;
(2)若f(6)=1,解不等式f(x+5)-f(
)≤2.
| x |
| y |
(1)求f(1)的值;
(2)若f(6)=1,解不等式f(x+5)-f(
| 1 |
| x |
(1)令x=y=1,则有f(1)=f(1)-f(1)=0;
(2)∵对一切x,y>0满足f(
)=f(x)-f(y)即f(
)+f(y)=f(x),
∴对一切x,y>0满足f(x)+f(y)=f(x•y),
又∵f(6)=1∴2=f(6)+f(6)=f(36);
∵f(x)是定义在(0,+∞)上的增函数,
∴f(x+5)-f(
)≤2?
?
?
?0<x≤4
故不等式f(x+5)-f(
)≤2的解集为:(0,4].
(2)∵对一切x,y>0满足f(
| x |
| y |
| x |
| y |
∴对一切x,y>0满足f(x)+f(y)=f(x•y),
又∵f(6)=1∴2=f(6)+f(6)=f(36);
∵f(x)是定义在(0,+∞)上的增函数,
∴f(x+5)-f(
| 1 |
| x |
|
|
?
|
故不等式f(x+5)-f(
| 1 |
| x |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
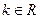 ,函数
,函数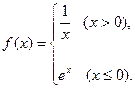 ,
,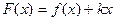 ,
,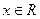 .
.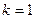 时,求
时,求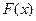 的值域;
的值域;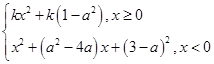 ,其中a∈R.若对任意的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得f(x2)=f(x1)成立,则实数k的取值范围是________.
,其中a∈R.若对任意的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得f(x2)=f(x1)成立,则实数k的取值范围是________.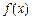 满足
满足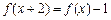 ,则
,则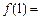 ( )
( )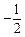 D.
D.