题目内容
【题目】已知函数f(x)满足f(x+y)=f(x)·f(y),且f(1)=![]() .
.
(1)当n∈N+,求f(n)的表达式;
(2)设an=nf(n),n∈N+,求证:a1+a2+…+an<2.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)利用f(x+y)=f(x)f(y)(x,y∈R)通过令x=n,y=1,说明{f(n)}是以f(1)=![]() 为首项,公比为
为首项,公比为![]() 的等比数列求出
的等比数列求出![]() ;(2)利用(1)求出an=nf(n)的表达式,利用错位相减法求出数列的前n项和,即可说明不等式成立.
;(2)利用(1)求出an=nf(n)的表达式,利用错位相减法求出数列的前n项和,即可说明不等式成立.
(1)解:f(n)=f[(n-1)+1]
=f(n-1)·f(1)=![]() f(n-1).
f(n-1).
∴当n≥2时,![]() =
=![]() .
.
又f(1)=![]() ,
,
∴数列{f(n)}是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,
∴f(n)=f(1)·(![]() )n-1=(
)n-1=(![]() )n.
)n.
(2)证明:由(1)可知,
an=n·(![]() )n=n·
)n=n·![]() ,
,
设Sn=a1+a2+…+an,
则Sn=![]() +2×
+2×![]() +3×
+3×![]() +…+(n-1)·
+…+(n-1)·![]() +n·
+n·![]() ,①
,①
∴![]() Sn=
Sn=![]() +2×
+2×![]() +…+(n-2)·
+…+(n-2)·![]() +(n-1)·
+(n-1)·![]() +n·
+n·![]() .②
.②
①-②得,
![]() Sn=
Sn=![]() +
+![]() +
+![]() +…+
+…+![]() -n·
-n·![]()
=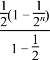 -
-![]() =1-
=1-![]() -
-![]() ,
,
∴Sn=2-![]() -
-![]() <2.
<2.
即a1+a2+…+an<2.
【点睛】
本题考查数列与函数的关系,数列通项公式的求法和的求法,考查不等式的证明,裂项法与错位相减法的应用,数列通项的求法中有常见的已知![]() 和
和![]() 的关系,求
的关系,求![]() 表达式,一般是写出
表达式,一般是写出![]() 做差得通项,但是这种方法需要检验n=1时通项公式是否适用;数列求和常用法有:错位相减,裂项求和,分组求和等.
做差得通项,但是这种方法需要检验n=1时通项公式是否适用;数列求和常用法有:错位相减,裂项求和,分组求和等.
【题型】解答题
【结束】
22
【题目】设数列{an}的前n项和为Sn.已知a1=a (a≠3),an+1=Sn+3n,n∈N+.
(1)设bn=Sn-3n,求数列{bn}的通项公式;
(2)若an+1≥an,n∈N+,求a的取值范围.
【答案】(1)bn= (a-3)2n-1(2)[-9,+∞).
【解析】
(Ⅰ)由题意可知bn=Sn-3n,Sn+1-Sn=an+1=Sn+3n,即Sn+1=2Sn+3n,得Sn+1-3n+1=2(Sn-3n),bn+1=2bn,则{bn}是首项是a﹣3,公比为2的等比数列,即可求得数列{bn}的通项公式;(Ⅱ)先求得数列an通项an=2×3n-1+(a-3)2n-2,将数列表达式代入不等式an+1≥an,得到a≥3-12·(![]() )n-2根据指数的单调性得到a的范围.
)n-2根据指数的单调性得到a的范围.
(1)依题意,Sn+1-Sn=an+1=Sn+3n,
即Sn+1=2Sn+3n,
由此得Sn+1-3n+1=2(Sn-3n),即{Sn-3n}是以a-3为首项,以2为公比的等比数列.
因此,所求通项公式为bn=Sn-3n=(a-3)2n-1,n∈N+.①
(2)由①知Sn=3n+(a-3)2n-1,n∈N+,
于是,当n≥2时,an=Sn-Sn-1
=3n+(a-3)×2n-1-3n-1-(a-3)×2n-2
=2×3n-1+(a-3)2n-2,
an+1-an=4×3n-1+(a-3)2n-2
=2n-2[12·(![]() )n-2+a-3],
)n-2+a-3],
当n≥2时,an+1≥an12·(![]() )n-2+a-3≥0
)n-2+a-3≥0
a≥3-12·(![]() )n-2a≥-9.
)n-2a≥-9.
又a2=a1+3>a1,
综上,所求的a的取值范围是[-9,+∞).