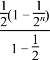Question

【题目】已知f（x）=2|x+1|﹣|x﹣1|．
（1）画出函数f（x）的图象；
（2）解不等式|f（x）|＞1．

Answer 1

【答案】
（1）解：当x≥1时，f（x）=2（x+1）﹣（x﹣1）=x+3；

当﹣1＜x＜1时，f（x）=2（x+1）﹣（1﹣x）=3x+1；

当x≤﹣1时，f（x）=﹣2（x+1）+（x﹣1）=﹣x﹣3，

所以

（2）解：根据图象可得|f（x）|=1时，x=﹣4或﹣1或 或0，

所以|f（x）|＞1的解集为 ．

【解析】（1）确定分段函数，即可画出函数f（x）的图象；（2）根据图象可得|f（x）|=1时，x=﹣4或﹣1或 或0，即可解不等式|f（x）|＞1．
【考点精析】根据题目的已知条件，利用绝对值不等式的解法的相关知识可以得到问题的答案，需要掌握含绝对值不等式的解法：定义法、平方法、同解变形法，其同解定理有；规律：关键是去掉绝对值的符号．