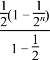Question

【题目】已知x=3是函数f（x）=aln（1+x）+x2﹣10x的一个极值点．
（Ⅰ）求a；
（Ⅱ）求函数f（x）的单调区间；
（Ⅲ）若直线y=b与函数y=f（x）的图象有3个交点，求b的取值范围．

Answer 1

【答案】解：（Ⅰ）因为 所以
因此a=16
（Ⅱ）由（Ⅰ）知，f（x）=16ln（1+x）+x2﹣10x，x∈（﹣1，+∞）
当x∈（﹣1，1）∪（3，+∞）时，f′（x）＞0
当x∈（1，3）时，f′（x）＜0
所以f（x）的单调增区间是（﹣1，1），（3，+∞）f（x）的单调减区间是（1，3）
（Ⅲ）由（Ⅱ）知，f（x）在（﹣1，1）内单调增加，
在（1，3）内单调减少，在（3，+∞）上单调增加，且当x=1或x=3时，f′（x）=0
所以f（x）的极大值为f（1）=16ln2﹣9，极小值为f（3）=32ln2﹣21
因此f（16）＞162﹣10×16＞16ln2﹣9=f（1）f（e﹣2﹣1）＜﹣32+11=﹣21＜f（3）
所以在f（x）的三个单调区间（﹣1，1），（1，3），（3，+∞）直线y=b有y=f（x）的图象各有一个交点，当且仅当f（3）＜b＜f（1）
因此，b的取值范围为（32ln2﹣21，16ln2﹣9）
【解析】（Ⅰ）先求导 ，再由x=3是函数f（x）=aln（1+x）+x2﹣10x的一个极值点即 求解．（Ⅱ）由（Ⅰ）确定f（x）=16ln（1+x）+x2﹣10x，x∈（﹣1，+∞）再由f′（x）＞0和f′（x）＜0求得单调区间．
（Ⅲ）由（Ⅱ）知，f（x）在（﹣1，1）内单调增加，在（1，3）内单调减少，在（3，+∞）上单调增加，且当x=1或x=3时，f′（x）=0，可得f（x）的极大值为f（1），极小值为f（3）一，再由直线y=b与函数y=f（x）的图象有3个交点则须有f（3）＜b＜f（1）求解，因此，b的取值范围为（32ln2﹣21，16ln2﹣9）．