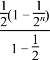题目内容
【题目】设a∈R,函数f(x)=x|x﹣a|﹣a.
(1)若f(x)为奇函数,求a的值;
(2)若对任意的x∈[2,3],f(x)≥0恒成立,求a的取值范围;
(3)当a>4时,求函数y=f(f(x)+a)零点的个数.
【答案】
(1)解:∵f(x)在原点有定义,f(x)为奇函数;
∴f(0)=﹣a=0;
∴a=0
(2)解:f(x)=x|x﹣a|﹣a;
∴①若a<2,则x=2时,f(x)在[2,3]上取得最小值f(2)=2(2﹣a)﹣a=4﹣3a;
∴4﹣3a≥0,a≤ ![]() ;
;
∴ ![]() ;
;
②若2≤a≤3,则x=a时,f(x)取得最小值f(a)=﹣a;
﹣a<0,不满足f(x)≥0;
即这种情况不存在;
③若a>3,则x=3时,f(x)取得最小值f(3)=3(a﹣3)﹣a=2a﹣9;
∴2a﹣9≥0,a ![]() ;
;
∴ ![]() ;
;
∴综上得a的取值范围为(﹣∞, ![]() ]∪[
]∪[ ![]() ,+∞)
,+∞)
(3)解:f(x)+a=x|x﹣a|,令x|x﹣a|=t;
∴y=t|t﹣a|﹣a;
下面作出函数t=x|x﹣a|= 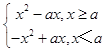 和函数y=t|t﹣a|﹣a=
和函数y=t|t﹣a|﹣a= 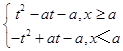 的图象:
的图象:
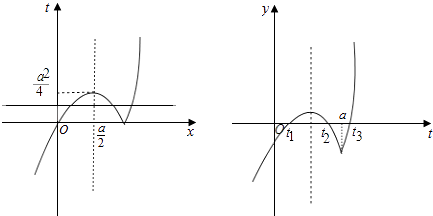
函数y=t|t﹣a|﹣a的图象可以认为由函数y=t|t﹣a|的图象向下平移a个单位得到;
显然函数y=t|t﹣a|﹣a的左边两个零点t=t1,t=t2都在(0,a)区间上,而通过t=x|x﹣a|的图象可看出:
∵ ![]() ,∴
,∴ ![]() ;
;
∴t1,t2分别有三个x和它对应;
∴这时原函数有6个零点;
由t(t﹣a)﹣a=t2﹣ta﹣a=0可以解出 ![]() ;
;
∴ 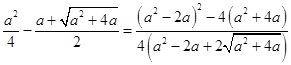 ;
;
显然 ![]() ;
;
而(a2﹣2a)2﹣4(a2+4a)=a[a2(a﹣4)﹣16];
显然a2(a﹣4)﹣16可能大于0,可能等于0,可能小于0;
∴t3可能和它对应的x个数为3,2,1;
∴此时原函数零点个数为3,2,或1;
∴原函数的零点个数为9个,8个,或7个
【解析】(1)根据f(0)=0即可求出a;(2)讨论a的取值:a<2,2≤a≤3,a>3,三种情况,求出每种情况下的f(x)的最小值,让最小值大于等于0从而求出a的取值范围;(3)代入f(x),原函数变成y=f(x|x﹣a|),这时候换元t=x|x﹣a|,y=t|t﹣a|﹣a.然后画出函数t=x|x﹣a|和函数y=t|t﹣a|﹣a的图象,通过图象找出有几个t使得y=t|t﹣a|﹣a=0,并找出对应的x的个数,从而找到原函数的零点个数.
【考点精析】解答此题的关键在于理解函数奇偶性的性质的相关知识,掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.

 小夫子全能检测系列答案
小夫子全能检测系列答案【题目】设△ABC是边长为4的正三角形,点P1 , P2 , P3 , 四等分线段BC(如图所示) 
(1)P为边BC上一动点,求 ![]()
![]() 的取值范围?
的取值范围?
(2)Q为线段AP1上一点,若 ![]() =m
=m ![]() +
+ ![]()
![]() ,求实数m的值.
,求实数m的值.
【题目】若关于某设备的使用年限x(年)和所支出的维修费y(万元)有如下统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知,y对x呈线性相关关系.
(1) 请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]()
![]() ;
;
(2) 估计使用年限为10年时,试求维修费用约是多少?(精确到两位小数)