题目内容
【题目】已知集合M是满足下列性制的函数f(x)的全体,存在实数a、k(k≠0),对于定义域内的任意x均有f(a+x)=kf(a﹣x)成立,称数对(a,k)为函数f(x)的“伴随数对”.
(1)判断f(x)=x2是否属于集合M,并说明理由;
(2)若函数f(x)=sinx∈M,求满足条件的函数f(x)的所有“伴随数对”;
(3)若(1,1),(2,﹣1)都是函数f(x)的“伴随数对”,当1≤x<2时,f(x)=cos( ![]() x);当x=2时,f(x)=0,求当2014≤x≤2016时,函数y=f(x)的解析式和零点.
x);当x=2时,f(x)=0,求当2014≤x≤2016时,函数y=f(x)的解析式和零点.
【答案】
(1)解:f(x)=x2的定义域为R.
假设存在实数a、k(k≠0),对于定义域内的任意x均有f(a+x)=kf(a﹣x)成立,
则(a+x)2=k(a﹣x)2,化为:(k﹣1)x2﹣2a(k+1)x+a2(k﹣1)=0,
由于上式对于任意实数x都成立,∴ 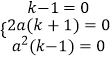 ,解得k=1,a=0.
,解得k=1,a=0.
∴(0,1)是函数f(x)的“伴随数对”,f(x)∈M
(2)解:∵函数f(x)=sinx∈M,
∴sin(a+x)=ksin(a﹣x),∴(1+k)cosasinx+(1﹣k)sinacosx=0,
∴ ![]() sin(x+φ)=0,
sin(x+φ)=0,
∵x∈R都成立,∴k2+2kcos2a+1=0,
∴cos2a= ![]() ,
, ![]() ≥2,
≥2,
∴|cos2a|≥1,又|cos2a|≤1,
故|cos2a|=1.
当k=1时,cos2a=﹣1,a=nπ+ ![]() ,n∈Z.
,n∈Z.
当k=﹣1时,cos2a=1,a=nπ,n∈Z.
∴f(x)的“伴随数对”为(nπ+ ![]() ,1),(nπ,﹣1),n∈Z
,1),(nπ,﹣1),n∈Z
(3)解:∵(1,1),(2,﹣1)都是函数f(x)的“伴随数对”,
∴f(1+x)=f(1﹣x),f(2+x)=﹣f(2﹣x),
∴f(x+4)=f(x),T=4.
当0<x<1时,则1<2﹣x<2,此时f(x)=f(2﹣x)=﹣cos ![]() ;
;
当2<x<3时,则1<4﹣x<2,此时f(x)=﹣f(4﹣x)=﹣cos ![]() ;
;
当3<x<4时,则0<4﹣x<1,此时f(x)=﹣f(4﹣x)=cos ![]() .
.
∴f(x)= 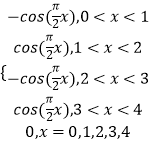 .
.
∴f(x)= 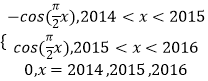 .
.
∴当2014≤x≤2016时,函数y=f(x)的零点为2014,2015,2016
【解析】(1)f(x)=x2的定义域为R.假设存在实数a、k(k≠0),对于定义域内的任意x均有f(a+x)=kf(a﹣x)成立,则(a+x)2=k(a﹣x)2 , 化为:(k﹣1)x2﹣2a(k+1)x+a2(k﹣1)=0,由于上式对于任意实数x都成立,可得 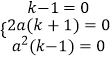 ,解得k,a.即可得出.(2)函数f(x)=sinx∈M,可得:sin(a+x)=ksin(a﹣x),展开化为:
,解得k,a.即可得出.(2)函数f(x)=sinx∈M,可得:sin(a+x)=ksin(a﹣x),展开化为: ![]() sin(x+φ)=0,由于x∈R都成立,可得k2+2kcos2a+1=0,变形cos2a=
sin(x+φ)=0,由于x∈R都成立,可得k2+2kcos2a+1=0,变形cos2a= ![]() ,利用基本不等式的性质与三角函数的单调性即可得出.(3)由于(1,1),(2,﹣1)都是函数f(x)的“伴随数对”,可得f(1+x)=f(1﹣x),f(2+x)=﹣f(2﹣x),因此f(x+4)=f(x),T=4.对x分类讨论可得:即可得出解析式,进而得出零点.
,利用基本不等式的性质与三角函数的单调性即可得出.(3)由于(1,1),(2,﹣1)都是函数f(x)的“伴随数对”,可得f(1+x)=f(1﹣x),f(2+x)=﹣f(2﹣x),因此f(x+4)=f(x),T=4.对x分类讨论可得:即可得出解析式,进而得出零点.
【考点精析】本题主要考查了函数的值的相关知识点,需要掌握函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法才能正确解答此题.