Question

【题目】已知函数 ．
（1）求函数y=f（x）的周期，并写出其单调递减区间；
（2）当 时，求f（x）的最大值与最小值．

Answer 1

【答案】
（1）解：函数 ．

化简可得：

=

=

= ，

即

函数的周期T= ．

由2kπ+

得k

∴f（x）的单调递减区间为 ．

（2）解：当x 时，

2x+ ，

∴ ≤sin（2x+ ）≤1．

故f（x）取得最大值 ；f（x）取得最小值 ．

【解析】（1）根据两角和的正弦公式和二倍角的余弦公式将f（x）进行化简可得f ( x ) = s i n ( 2 x + ) + 1，根据周期公式和正弦函数的单调区间即可得出，（2）根据正弦函数的性质即可在给定区间得出f（x）的最大值和最小值.
【考点精析】关于本题考查的三角函数的最值，需要了解函数，当时，取得最小值为；当时，取得最大值为，则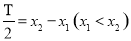，，才能得出正确答案．