题目内容
【题目】某旅游公司为甲,乙两个旅游团提供四条不同的旅游线路,每个旅游团可任选其中一条旅游线路.
(1)求甲、乙两个旅游团所选旅游线路不同的概率;
(2)某天上午9时至10时,甲,乙两个旅游团都到同一个著名景点游览,20分钟后游览结束即离去.求两个旅游团在该著名景点相遇的概率.
【答案】
(1)解:某旅游公司为甲,乙两个旅游团提供四条不同的旅游线路,
每个旅游团可任选其中一条旅游线路,基本事件总数n=42=16,
甲、乙两个旅游团所选旅游线路不同包含的基本事件个数m= ![]() =4×3=12,
=4×3=12,
∴甲、乙两个旅游团所选旅游线路不同的概率:
p= ![]()
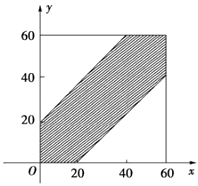
(2)解:设甲、乙两个旅游团到达著名景点的时刻分别为x,y,
依题意得  ,即
,即 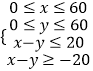 ,
,
作出不等式表示的区域,如图:
记“两个旅游团在著名景点相遇”为事件B,
P(B)= ![]() =
= ![]() .
.
∴两个旅游团在该著名景点相遇的概率为 ![]() .
.
【解析】(1)每个旅游团可任选其中一条旅游线路,基本事件总数n=42=16,甲、乙两个旅游团所选旅游线路不同包含的基本事件个数m= ![]() =4×3=12,由此能求出甲、乙两个旅游团所选旅游线路不同的概率.(2)设甲、乙两个旅游团到达著名景点的时刻分别为x,y,依题意得
=4×3=12,由此能求出甲、乙两个旅游团所选旅游线路不同的概率.(2)设甲、乙两个旅游团到达著名景点的时刻分别为x,y,依题意得  ,由此利用几何概型能求出两个旅游团在该著名景点相遇的概率.
,由此利用几何概型能求出两个旅游团在该著名景点相遇的概率.
【考点精析】解答此题的关键在于理解几何概型的相关知识,掌握几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等.

练习册系列答案
相关题目
