题目内容
【题目】已知定义在R上的奇函数f(x),满足f(x﹣2)=﹣f(x),且当x∈[0,1]时,f(x)=x2+x+sinx,若方程f(x)=m(m>0)在区间[﹣4,4]上有四个不同的根x1 , x2 , x3 , x4 , 则x1+x2+x3+x4的值为( )
A.2
B.﹣2
C.4
D.﹣4
【答案】D
【解析】解:∵f(x﹣2)=﹣f(x),
∴f(x﹣4)=﹣f(x﹣2)=f(x),
即函数的周期是4,
且f(x﹣2)=﹣f(x)=f(﹣x),
则函数的对称轴为:x=﹣1,f(x)是奇函数,
所以x=1也是对称轴,x∈[0,1]时,f(x)=x2+x+sinx,
函数是增函数,
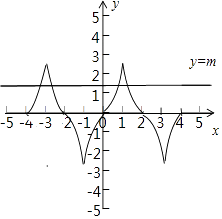
作出函数f(x)的简图,
若方程f(x)=m(m>0)在区间[﹣4,4]上
有四个不同的根x1,x2,x3,x4,
则四个根分别关于x=1和x=3对称,
不妨设x1<x2<x3<x4,
则x1+x2=﹣6,x3+x4=2,
则x1+x2+x3+x4=﹣6+2=﹣4,
所以答案是:D.

练习册系列答案
相关题目