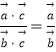题目内容
【题目】已知函数f(x)=x2﹣2x﹣2
(Ⅰ)用定义法证明:函数f(x)在区间(﹣∞,1]上是减函数;
(Ⅱ)若函数g(x)=f(x)﹣mx是偶函数,求m的值.
【答案】解:(Ⅰ)设﹣∞<x1<x2≤1,
所以,f(x1)﹣f(x2)=( ![]() ﹣2x1﹣2)﹣(
﹣2x1﹣2)﹣( ![]() ﹣2x2﹣2)=(x1﹣x2 )(x1+x2﹣2),
﹣2x2﹣2)=(x1﹣x2 )(x1+x2﹣2),
因为﹣∞<x1<x2,所以,x1﹣x2<0,x1+x2﹣2<0,
所以,f(x1)﹣f(x2)>0,
所以,f(x1)>f(x2),
所以函数f(x)在区间(﹣∞,1]上是减函数.
(Ⅱ)因为函数g(x)=f(x)﹣mx=x2﹣(2+m)x﹣2,
又因为g(x)是偶函数,2+m=0,
∴m=﹣2.
【解析】(1)根据定义法进行设值作差变形整理可得,(2)当g(x)为偶函数时,其二次函数的对称轴为y轴,即2+m=0,即可解得m=-2.
【考点精析】根据题目的已知条件,利用函数奇偶性的性质和二次函数在闭区间上的最值的相关知识可以得到问题的答案,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇;当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() .
.

练习册系列答案
相关题目