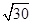题目内容
设抛物线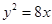 上一点P到y轴的距离是4,则点P到该抛物线的焦点的距离是 ( )
上一点P到y轴的距离是4,则点P到该抛物线的焦点的距离是 ( )
| A.6 | B.4 | C.8 | D.12 |
A
解析试题分析:由抛物线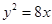 知,点P到y轴的距离是4,那么P到抛物线准线距离为6,又由抛物线定义“到准线距离与到焦点距离相等”,所以点P到该抛物线的焦点的距离是6,故选A。
知,点P到y轴的距离是4,那么P到抛物线准线距离为6,又由抛物线定义“到准线距离与到焦点距离相等”,所以点P到该抛物线的焦点的距离是6,故选A。
考点:本题主要考查抛物线的定义及其几何性质。
点评:简单题,涉及抛物线上的到焦点距离问题,一般要考虑应用抛物线定义“到准线距离与到焦点距离相等”。

练习册系列答案
相关题目
已知 ,
,  是椭圆
是椭圆 的两个焦点,点
的两个焦点,点 在此椭圆上且
在此椭圆上且 ,则
,则 的面积等于( )
的面积等于( )
A. | B. | C.2 | D. |
已知抛物线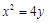 的焦点
的焦点 和点
和点 为抛物线上一点,则
为抛物线上一点,则 的最小值是( )
的最小值是( )
| A.3 | B.9 | C.12 | D.6 |
双曲线 -
-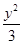 =1的渐近线与圆(x-3)2+y2=r2(r>0)相切,则r=( )
=1的渐近线与圆(x-3)2+y2=r2(r>0)相切,则r=( )
A. | B.2 | C.3 | D.6 |
椭圆 的焦点坐标是( )
的焦点坐标是( )
A.(0, )、(0, )、(0, ) ) | B. (0,-1)、(0,1) |
| C.(-1,0)、(1,0) | D.( ,0)、( ,0)、( ,0) ,0) |
一动圆圆心在抛物线 上,且动圆恒与直线
上,且动圆恒与直线 相切,则动圆必过定点
相切,则动圆必过定点
A.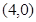 | B. | C. | D. |
 ,
, ,曲线上的点P到
,曲线上的点P到 、
、 的距离之差的绝对值是6,则该曲线的方程为( )
的距离之差的绝对值是6,则该曲线的方程为( )


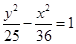
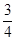

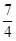
 ,
, ),P2的柱坐标是P2(2,
),P2的柱坐标是P2(2, ,1),则|P1P2|=( )
,1),则|P1P2|=( )