题目内容
已知点P1的球坐标是P1(4，
，
)，P2的柱坐标是P2(2，
，1)，则|P1P2|=( )
A． | B． | C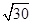． | D． |
A
解析试题分析：点P1的球坐标是P1(4，，)
，
P2的柱坐标是
P2(2，，1)
考点：柱坐标极坐标与直角坐标的互相转化
点评：三种坐标转化的基本公式要掌握
练习册系列答案
作业辅导系列答案
相关题目
设抛物线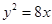
上一点P到y轴的距离是4，则点P到该抛物线的焦点的距离是 ( )
| A．6 | B．4 | C．8 | D．12 |
过点
，且与
有相同渐近线的双曲线方程是
A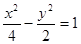． | B． |
C． | D． |
抛物线 
的准线方程是（ ）
| A．4 x + 1 = 0 | B．4 y + 1 =" 0" |
| C．2 x + 1 = 0 | D．2 y + 1 =" 0" |
已知点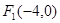
和
，曲线上的动点P到
、
的距离之差为6，则曲线方程为（）
A． | B． |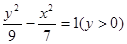
C．或 | D． |
抛物线
上一点P到
轴的距离是4，则点P到该抛物线焦点的距离是( )
| A．4 | B．6 | C．8 | D．12 |
若直线
与曲线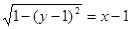
有两个不同的交点，则实数
的取值范围是（ ）
A． | B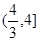． | C． | D． |
抛物线y2=2px(p>0)上有一点M，它的横坐标是3,它到焦点的距离是5,则抛物线方程为( A )
| A．y2=8x | B．y2=4x | C．y2=3x | D．y2=2x |
