题目内容

如图，海中小岛A周围40海里内有暗礁，一船正在向南航行，在B处测得小岛A在船的南偏东30°，航行30海里后，在C处测得小岛在船的南偏东45°，如果此船不改变航向，继续向南航行，问有无触礁的危险？
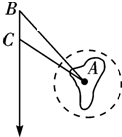
在△ABC中，BC=30，∠B=30°，∠C=135°，所以∠A=15°，
根据正弦定理
BC
sinA
=
AC
sinB
得：
30
sin15°
=
AC
sin30°
，
∴AC=
30sin30°
sin15°
=60cos15°=60cos（45°-30°）=60（cos45°cos30°+sin45°sin30°）=15（
6
+
2
），
∴A到BC边所在直线的距离为：ACsin45°=15（
6
+
2
）×
2
2
=15（
3
+1）≈40.98（海里），
∵40.98＞40，
∴船继续向南航行没有触礁的危险，
则此船不改变航向，继续向南航行，无触礁的危险．
练习册系列答案
相关题目

（2）试借助诱导公式证明△A2B2C2中必有一个角为钝角
已知△ABC的三边a，b，c和其面积S满足S=c2-（a-b）2且a+b=2，则S的最大值为（　　）
A．
8
17
B．
6
17
C．
5
17
D．
4
17
海上两个小岛A、B到海洋观察站C的距离都是akm，小岛A在观察站C北偏东20°，小岛B在观察站C南偏东40°，则A与B的距离是（　　）
A．akmB．
3
akm		C．
2
akm		D．2akm
△ABC中，已知（a+b+c）（b+c-a）=bc，则A的度数等于（　　）
A．120°B．60°C．150°D．30°
在△ABC中，若三边a、b、c满足（a+b-c）（a+b+c）=ab．则角C=（　　）
A．
2π
3
B．
π
3
C．
π
6
D．
2π
3
或
π
3
在三角形ABC中，AB=5，AC=3，BC=7，则∠BAC的大小为（　　）
A．30°B．60°C．90°D．120°
在△ABC中，内角A，B，C的对边分别为a，b，c，且满足c=2acosB，则△ABC的形状是（　　）
A．等腰三角形
B．直角三角形
C．等腰直角三角形
D．等腰三角形或直角三角形
已知△ABC中，角A，B，C所对的边分别是a，b，c，且2（a2+b2-c2）=3ab；
（1）求sin2
A+B
2
；
（2）若c=2，求△ABC面积的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网