题目内容
(2)试借助诱导公式证明△A2B2C2中必有一个角为钝角
(1)是锐角三角形
(1)由条件知△A1B1C1的三个内角的余弦值均大于0,
即cosA1﹥0, cosB1﹥0, cosC1﹥0,从而△A1B1C1一定是锐角三角形。
(2)、由题意知:sinA2=cosA1=sin(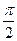 -A1), sinB2=cosB1=sin(
-A1), sinB2=cosB1=sin(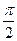 -B1),sinC2=cosC1=sin(
-B1),sinC2=cosC1=sin(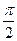 -C1).
-C1).
若A2、B2、C2全为锐角,A2+B2+C2=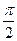 -A1+
-A1+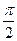 -B1+
-B1+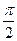 -C1=
-C1=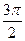 -( A1+B1+C1)=
-( A1+B1+C1)=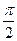 .不合题
.不合题
意,应舍去。又A2、B2、C2不可能为直角,且满足A2+B2+C2=。故必有一角为钝角
即cosA1﹥0, cosB1﹥0, cosC1﹥0,从而△A1B1C1一定是锐角三角形。
(2)、由题意知:sinA2=cosA1=sin(
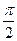 -A1), sinB2=cosB1=sin(
-A1), sinB2=cosB1=sin(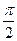 -B1),sinC2=cosC1=sin(
-B1),sinC2=cosC1=sin(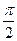 -C1).
-C1).若A2、B2、C2全为锐角,A2+B2+C2=
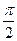 -A1+
-A1+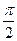 -B1+
-B1+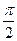 -C1=
-C1=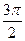 -( A1+B1+C1)=
-( A1+B1+C1)=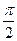 .不合题
.不合题意,应舍去。又A2、B2、C2不可能为直角,且满足A2+B2+C2=。故必有一角为钝角

练习册系列答案
相关题目
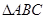 中,
中, 的面积
的面积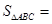
 则
则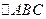 的面积等于
的面积等于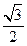
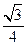
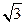
 中,
中, 分别为角
分别为角 的对边,且满足
的对边,且满足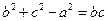 .
. 的值;
的值; ,设角
,设角 的大小为
的大小为
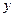 ,求
,求 的最大值.
的最大值.
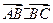 = ..
= ..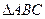 中已知两边a=1,b=2,则第三边c的取值范围是_________
中已知两边a=1,b=2,则第三边c的取值范围是_________