题目内容
7.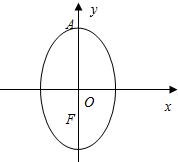 已知动圆Q过定点F(0,-1),且与直线l:y=1相切,椭圆N的对称轴为坐标轴,O点为坐标原点,F是其一个焦点,又点A(0,2)在椭圆N上.
已知动圆Q过定点F(0,-1),且与直线l:y=1相切,椭圆N的对称轴为坐标轴,O点为坐标原点,F是其一个焦点,又点A(0,2)在椭圆N上.(Ⅰ)求动圆圆心Q的轨迹M的标准方程和椭圆N的标准方程;
(Ⅱ)若过F的动直线m交椭圆N于B,C点,交轨迹M于D,E两点,设S1为△ABC的面积,S2为△ODE的面积,令Z=S1S2,试求Z的最小值.
分析 (Ⅰ)由抛物线的定义可得动点Q的轨迹M的标准方程,由题意可得c=1,a=2,求得b,进而得到椭圆方程;
(Ⅱ)显然直线m的斜率存在,不妨设直线m的直线方程为:y=kx-1,分别代入抛物线方程和椭圆方程,运用韦达定理和弦长公式,以及点到直线的距离公式,求得三角形的面积,再由不等式的性质,即可得到所求最小值.
解答 解:(Ⅰ)依题意,由抛物线的定义易得动点Q的轨迹M的标准方程为:x2=-4y,
依题意可设椭圆N的标准方程为$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1(a>b>0)$,
显然有$c=1,a=2∴b=\sqrt{3}$,
∴椭圆N的标准方程为$\frac{y^2}{4}+\frac{x^2}{3}=1$;
(Ⅱ)显然直线m的斜率存在,
不妨设直线m的直线方程为:y=kx-1①
联立椭圆N的标准方程$\frac{y^2}{4}+\frac{x^2}{3}=1$有(3k2+4)x2-6kx-9=0,
设B(x1,y1),C(x2,y2)
则有$|{BC}|=\sqrt{1+{k^2}}|{{x_1}-{x_2}}|=\sqrt{1+{k^2}}\frac{{12\sqrt{1+{k^2}}}}{{3{k^2}+4}}=\frac{{12(1+{k^2})}}{{3{k^2}+4}}$,
又A(0,2)到直线m的距离${d_1}=\frac{3}{{\sqrt{1+{k^2}}}}$,
∴${S_1}=\frac{1}{2}|{BC}|{d_1}=\frac{{18\sqrt{1+{k^2}}}}{{3{k^2}+4}}$,
再将①式联立抛物线方程x2=-4y有x2+4kx-4=0,
同理易得$|{DE}|=4(1+{k^2}),{d_2}=\frac{1}{{\sqrt{1+{k^2}}}}$,
∴${S_2}=2\sqrt{1+{k^2}}$,
∴$Z={S_1}{S_2}=\frac{{36(1+{k^2})}}{{3{k^2}+4}}=12(1-\frac{1}{{3{k^2}+4}})≥12(1-\frac{1}{4})=9$,
∴当k=0时,Zmin=9.
点评 本题考查直线和圆相切的条件,同时考查抛物线的定义和椭圆方程的运用,注意联立直线方程,运用韦达定理和弦长公式,考查化简整理的运算能力,属于中档题.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案| A. | $\frac{1}{4}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |