题目内容
2.在四边形ABCD中,∠B=∠D=90°,∠A=60°,AB=4,AD=5,求AC的长和$\frac{BC}{CD}$的值.分析 过点C作CE∥AD交AB于点E,再作EF∥CD交AD于点F,在Rt△AEF中,可将各边用含BC和CD的代数式表达出来,根据∠A=60°列出三角函数式代入求解.
解答  解:如图,过点C作CE∥AD交AB于点E,再作EF∥CD交AD于点F,
解:如图,过点C作CE∥AD交AB于点E,再作EF∥CD交AD于点F,
设BC=a,CD=b,
在Rt△BCE中,∵AD∥CE,
∴∠CEB=∠A=60°,
可得BE=cot∠CEB×BC=$\frac{\sqrt{3}}{3}$a,CE=$\sqrt{B{E}^{2}+B{C}^{2}}$=$\frac{2\sqrt{3}}{3}$a,
故AE=4-$\frac{\sqrt{3}}{3}$a,
∵四边形CDFE为矩形,
∴DF=CE=$\frac{2\sqrt{3}}{3}$a,
∴AF=5-$\frac{2\sqrt{3}}{3}$a,
在Rt△AEF中,
∵cos∠A=$\frac{AF}{AE}$=$\frac{1}{2}$,即$\frac{5-\frac{2\sqrt{3}}{3}a}{4-\frac{\sqrt{3}}{3}a}$=$\frac{1}{2}$,
∴a=2$\sqrt{3}$,
∴AC=$\sqrt{16+12}$=2$\sqrt{7}$.
sin∠A=$\frac{b}{4-\frac{\sqrt{3}}{3}a}$=$\frac{\sqrt{3}}{2}$,
∴b=$\sqrt{3}$
∵BC=a=2$\sqrt{3}$,CD=b=$\sqrt{3}$,
∴$\frac{BC}{CD}$=2.
点评 本题通过作辅助线可在直角三角形内进行求解,综合应用了解直角三角形、直角三角形性质,考查了逻辑推理能力和运算能力.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
10.记数列{an}的前n项和为Sn,且Sn=$\int_0^n$(2ax+b)dx(a,b常数).若不等式an2+$\frac{{S_{n}^2}}{{n{^2}}}$≥ma12对任意的数列{an}及任意正整数n都成立,则实数m的取值范围为( )
| A. | $(-∞,\frac{1}{2}]$ | B. | $[{\frac{1}{5},\frac{1}{2}}]$ | C. | $[{\frac{1}{5},+∞})$ | D. | $(-∞,\frac{1}{5}]$ |
7.若E,F,G,H分别在四面体的棱AB,BC,CD,AD上,且AC∥平面EFGH,则( )
| A. | EF∥GH | B. | EH∥FG | C. | EH∥平面BCD | D. | FG∥平面ABD |
19.已知函数y=f(x)的图象关于直线x=1对称,且在[1,+∞)上单调递减,f(0)=0,则f(x+1)>0的解集为( )
| A. | (1,+∞) | B. | (-1,1) | C. | (-∞,-1) | D. | (-∞,-1)∪(1,+∞) |
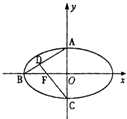 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率e=$\frac{3}{5}$,左焦点为F,A,B,C为其三个顶点,直线CF与AB交于点D,若△ADC的面积为15.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率e=$\frac{3}{5}$,左焦点为F,A,B,C为其三个顶点,直线CF与AB交于点D,若△ADC的面积为15.