题目内容
椭圆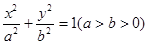 的两顶点为
的两顶点为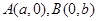 ,且左焦点为F,
,且左焦点为F,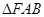 是以角B为直角的直角三角形,则椭圆的离心率
是以角B为直角的直角三角形,则椭圆的离心率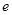 为 ( )
为 ( )
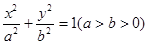 的两顶点为
的两顶点为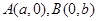 ,且左焦点为F,
,且左焦点为F,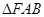 是以角B为直角的直角三角形,则椭圆的离心率
是以角B为直角的直角三角形,则椭圆的离心率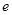 为 ( )
为 ( )A. | B. | C. | D. |
B
试题分析:依题意可知点F(-c,0)直线AB斜率为
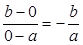 ,直线BF的斜率为
,直线BF的斜率为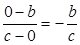 ,∵∠FBA=90°,∴(
,∵∠FBA=90°,∴( 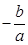 )•(
)•( 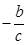 )
)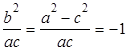 整理得
整理得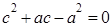 ,即
,即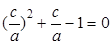 ,即e2-e-1=0,解得e=
,即e2-e-1=0,解得e= 或
或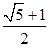 ∵e<1,∴e=
∵e<1,∴e= ,故选B.
,故选B.
练习册系列答案
相关题目
 ,
, 分别是椭圆
分别是椭圆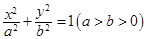 的左右焦点,M是C上一点且
的左右焦点,M是C上一点且 与x轴垂直,直线
与x轴垂直,直线 与C的另一个交点为N.
与C的另一个交点为N. ,求C的离心率;
,求C的离心率;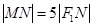 ,求a,b.
,求a,b. .
. 为圆O:
为圆O: 的弦AB的中点,则直线AB的斜率
的弦AB的中点,则直线AB的斜率 与直线OE的斜率
与直线OE的斜率 的乘积
的乘积 为定值。类比圆的这个性质,写出椭圆
为定值。类比圆的这个性质,写出椭圆 的类似性质,并加以证明;
的类似性质,并加以证明; 的切线
的切线 ,
, 上任意一点
上任意一点 作
作 上运动时,是否存在定圆恒与直线MN相切?若存在,求出圆的方程;若不存在,请说明理由.
上运动时,是否存在定圆恒与直线MN相切?若存在,求出圆的方程;若不存在,请说明理由.

 的左、右焦点分别为
的左、右焦点分别为 ,其上顶点为
,其上顶点为 已知
已知 是边长为
是边长为 的正三角形.
的正三角形.
 的方程;
的方程; 任作一动直线
任作一动直线 交椭圆
交椭圆 两点,记
两点,记 .若在线段
.若在线段 上取一点
上取一点 ,使得
,使得 ,当直线
,当直线
 或2
或2 2
2
 与椭圆
与椭圆 相交于
相交于 两点,点
两点,点 是线段
是线段 上的一点,
上的一点, 且点
且点 上.
上. 的对称点在单位圆
的对称点在单位圆 上,求椭圆的方程.
上,求椭圆的方程.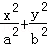 =1(a>b>0)与双曲线C2:x2﹣
=1(a>b>0)与双曲线C2:x2﹣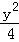 =1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
=1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )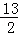

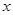 轴的椭圆
轴的椭圆
 的左、右焦点分别为
的左、右焦点分别为 ,直线
,直线 过右焦点
过右焦点 ,和椭圆交于
,和椭圆交于 两点,且满足
两点,且满足 ,
,  ,则椭圆
,则椭圆 的标准方程为( )
的标准方程为( )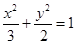



 :
: (
( )过点
)过点 ,且椭圆
,且椭圆 .
. 在直线
在直线 上,过
上,过 两点,且
两点,且 中点,再过
中点,再过 .求直线
.求直线 是否恒过定点,如果是则求出该定点的坐标,不是请说明理由。
是否恒过定点,如果是则求出该定点的坐标,不是请说明理由。