题目内容

20．设f（x）=$\left\{\begin{array}{l}{{2}^{x+1}（x≥0）}\\{f（x+1）+2（x＜0）}\end{array}\right.$，则f（-$\frac{2015}{2}$）=2$\sqrt{2}$+2016．

分析 由已知中f（x）=$\left\{\begin{array}{l}{{2}^{x+1}（x≥0）}\\{f（x+1）+2（x＜0）}\end{array}\right.$，将x=-$\frac{2015}{2}$代入，分析变量的变化规律，可得答案．

解答 解：∵f（x）=$\left\{\begin{array}{l}{{2}^{x+1}（x≥0）}\\{f（x+1）+2（x＜0）}\end{array}\right.$，
∴f（-$\frac{2015}{2}$）=f（-$\frac{2013}{2}$）+2=f（-$\frac{2011}{2}$）+2×2=…=f（-$\frac{1}{2}$）+2×1007=f（$\frac{1}{2}$）+2×1008=${2}^{\frac{3}{2}}$+2016=2$\sqrt{2}$+2016，
故答案为：2$\sqrt{2}$+2016．

点评 本题考查的知识点是分段函数的应用，函数求值，难度不大，属于基础题．

练习册系列答案
相关题目
10．设复数z1，z2满足条件|z1|=1，|z2|=2，则|z1-z2|的范围是[1，3]．
11．在△ABC中，内角A，B，C所对应的边分别为a，b，c，若bsinA-$\sqrt{3}$acosB=0，且b2=ac，则$\frac{b}{a+c}$的值为
（　　）
A．$\frac{\sqrt{2}}{2}$B．$\sqrt{2}$C．2D．$\frac{1}{2}$
8．在△ABC中，三个内角A，B，C的对边分别为a，b，c，其中c=2，且$\frac{cosA}{cosB}$=$\frac{b}{a}$=$\frac{\sqrt{3}}{1}$．
（Ⅰ）求a，b，C．
（Ⅱ）如右图，设圆O过A，B，C三点，点P位于劣弧$\widehat{AC}$上，记∠PAB=θ，求△PAC面积最大值．
15．已知f（x）=|x-2|-1，若直线y=m与函数y=f[f（x）]的图象有四个不同的交点，则实数m的取值范围是（　　）
A．（-1，2）B．（0，3）C．（-1，1）D．（-1，3）
5．设f（x）为定义在R上的奇函数，且是周期为4的周期函数，f（1）=1，则f（-1）+f（8）=（　　）
A．-2B．-1C．0D．1
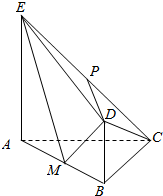12．如图，平面ABDE⊥平面ABC，AC⊥BC，AC=BC=4，四边形ABDE是直角梯形，BD∥AE，BD⊥BA，AE=2BD=4，P、M分别为CE，AB的中点．
（Ⅰ）证明：PD∥平面ABC；
（Ⅱ）是否在EM上存在一点N，使得PN⊥平面ABDE．若存在，请指出点N的位置，并加以证明；若不存在，请说明理由．
9．已知二次函数f（x）=x2-2ax+1在区间（2，3）上是单调函数，求实数a的取值范围．
10．已知向量$\overrightarrow{a}$=（1，-1）则下列向量中与向量$\overrightarrow{a}$平行且同向的是（　　）
A．（2，-2）B．（-2，2）C．（-1，2）D．（2，-1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网