题目内容
2.已知两点A(-m,0),B(m,0)(m>0),如果在直线3x+4y+25=0上存在点P,使得∠APB=90°,则m的取值范围是[5,+∞).分析 根据P在直线3x+4y+25=0上,设出点P的坐标,写出向量$\overrightarrow{AP}$、$\overrightarrow{BP}$;利用$\overrightarrow{AP}$•$\overrightarrow{BP}$=0得出方程,再由△≥0求出m的取值范围.
解答 解:∵P在直线3x+4y+25=0上,设点P(x,$\frac{-3x-25}{4}$),
∴$\overrightarrow{AP}$=(x+m,$\frac{-3x-25}{4}$),
$\overrightarrow{BP}$=(x-m,$\frac{-3x-25}{4}$);
又∠APB=90°,
∴$\overrightarrow{AP}$•$\overrightarrow{BP}$=(x+m)(x-m)+${(\frac{-3x-25}{4})}^{2}$=0,
即25x2+150x+625-16m2=0;
∴△≥0,
即1502-4×25×(625-16m2)≥0,
解得m≥5,或m≤-5,
又m>0,∴m的取值范围是[5,+∞).
故答案为:[5,+∞).
点评 本题考查了直线方程的应用问题,也考查了平面向量的数量积的应用问题,考查了转化思想的应用问题,是综合性题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.执行如图所示的程序框图,如果输入的x∈R,则输出的h(x)的最小值是( )


| A. | $\frac{3}{4}$ | B. | 3 | C. | 4 | D. | 7 |
11.在△ABC中,内角A,B,C所对应的边分别为a,b,c,若bsinA-$\sqrt{3}$acosB=0,且b2=ac,则$\frac{b}{a+c}$的值为
( )
( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
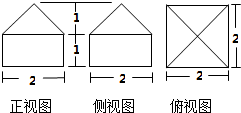 已知一几何体的三视图如图所示.
已知一几何体的三视图如图所示.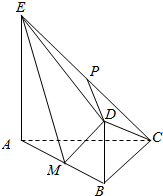 如图,平面ABDE⊥平面ABC,AC⊥BC,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,AE=2BD=4,P、M分别为CE,AB的中点.
如图,平面ABDE⊥平面ABC,AC⊥BC,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,AE=2BD=4,P、M分别为CE,AB的中点.