题目内容
已知函数f(x)=x3+f′ x2-x,则函数f(x)的图象在
x2-x,则函数f(x)的图象在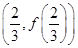 处的切线方程是 .
处的切线方程是 .
 x2-x,则函数f(x)的图象在
x2-x,则函数f(x)的图象在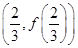 处的切线方程是 .
处的切线方程是 . 27x+27y+4=0
因为f′(x)=3x2+2f′ x-1,
x-1,
所以f′ =3×
=3× 2+2f′
2+2f′ ×
×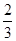 -1
-1
得f′ =-1,
=-1,
f =
= 3+f′
3+f′ ×
× 2-
2-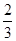
=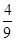 f′
f′ -
-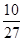
=-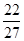 ,
,
则函数f(x)的图象在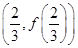 处的切线方程为
处的切线方程为
y+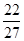 =-(x-
=-(x-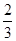 ),即27x+27y+4=0.
),即27x+27y+4=0.
 x-1,
x-1,所以f′
 =3×
=3× 2+2f′
2+2f′ ×
×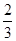 -1
-1得f′
 =-1,
=-1,f
 =
= 3+f′
3+f′ ×
× 2-
2-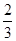
=
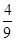 f′
f′ -
-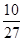
=-
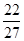 ,
,则函数f(x)的图象在
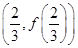 处的切线方程为
处的切线方程为y+
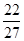 =-(x-
=-(x-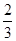 ),即27x+27y+4=0.
),即27x+27y+4=0.
练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
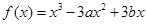 的图像与直线
的图像与直线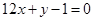 相切于点
相切于点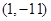 .
.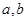 的值;
的值;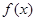 的单调性.
的单调性.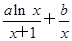 ,曲线y=f(x)在点(1,f(1))处的切线方程为x+2y-3=0.求a,b.
,曲线y=f(x)在点(1,f(1))处的切线方程为x+2y-3=0.求a,b.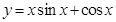 的图象上的点
的图象上的点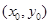 处的切线的斜率为k,若
处的切线的斜率为k,若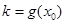 ,则函数
,则函数