题目内容
设f(x)=x+ax2+bln x,曲线y=f(x)过点
P(1,0),且在P点处的切线的斜率为2.
①求a,b的值;
②证明:f(x)≤2x-2.
P(1,0),且在P点处的切线的斜率为2.
①求a,b的值;
②证明:f(x)≤2x-2.
①a=-1,b=3.②见解析
① f′(x)=1+2ax+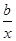 .
.
由题意知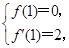 即
即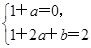 ,
,
解得a=-1,b=3.
②由①知f(x)=x-x2+3ln x.
f(x)的定义域为(0,+∞).
设g(x)=f(x)-(2x-2)=2-x-x2+3ln x,
则g′(x)=-1-2x+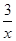 =-
=-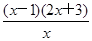 .?
.?
由g′(x)>0知0<x<1,
由g′(x)<0知x>1.
所以g(x)在(0,1)内单调递增,在(1,+∞)内单调递减.
所以g(x)在(0,+∞)上的最大值为g(1)=0,
所以g(x)≤0,即f(x)≤2x-2.
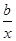 .
.由题意知
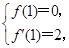 即
即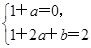 ,
,解得a=-1,b=3.
②由①知f(x)=x-x2+3ln x.
f(x)的定义域为(0,+∞).
设g(x)=f(x)-(2x-2)=2-x-x2+3ln x,
则g′(x)=-1-2x+
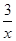 =-
=-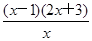 .?
.?由g′(x)>0知0<x<1,
由g′(x)<0知x>1.
所以g(x)在(0,1)内单调递增,在(1,+∞)内单调递减.
所以g(x)在(0,+∞)上的最大值为g(1)=0,
所以g(x)≤0,即f(x)≤2x-2.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
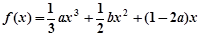 ,
,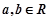 ,
,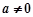 ,
, 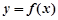 与
与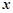 轴相切于异于原点的一点,且函数
轴相切于异于原点的一点,且函数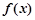 的极小值为
的极小值为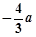 ,求
,求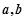 的值;
的值;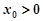 ,且
,且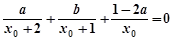 ,
,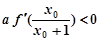 ; ②求证:
; ②求证: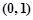 上存在极值点.
上存在极值点. 与商品单价的降低值
与商品单价的降低值 (单位:元,
(单位:元, )的平方成正比,已知商品单价降低1元时,一星期多卖出5件.
)的平方成正比,已知商品单价降低1元时,一星期多卖出5件. 表示成
表示成 在点
在点 处的切线与两坐标轴围成三角形的面积为
处的切线与两坐标轴围成三角形的面积为 ,则
,则 ________.
________. ex-f(0)x+
ex-f(0)x+ x2在点(1,f(1))处的切线方程为________.
x2在点(1,f(1))处的切线方程为________.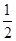 x+b是曲线y=lnx(x>0)的一条切线,则实数b=________.
x+b是曲线y=lnx(x>0)的一条切线,则实数b=________. x2-x,则函数f(x)的图象在
x2-x,则函数f(x)的图象在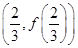 处的切线方程是 .
处的切线方程是 .