题目内容
已知抛物线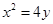 ,直线
,直线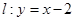 ,
,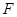 是抛物线的焦点。
是抛物线的焦点。
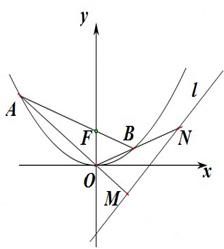
(1)在抛物线上求一点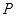 ,使点
,使点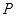 到直线
到直线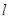 的距离最小;
的距离最小;
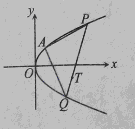
(2)如图,过点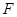 作直线交抛物线于A、B两点.
作直线交抛物线于A、B两点.
①若直线AB的倾斜角为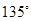 ,求弦AB的长度;
,求弦AB的长度;
②若直线AO、BO分别交直线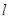 于
于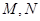 两点,求
两点,求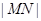 的最小值.
的最小值.
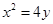 ,直线
,直线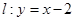 ,
,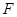 是抛物线的焦点。
是抛物线的焦点。
(1)在抛物线上求一点
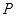 ,使点
,使点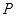 到直线
到直线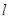 的距离最小;
的距离最小;(2)如图,过点
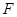 作直线交抛物线于A、B两点.
作直线交抛物线于A、B两点.①若直线AB的倾斜角为
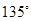 ,求弦AB的长度;
,求弦AB的长度;②若直线AO、BO分别交直线
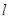 于
于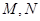 两点,求
两点,求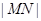 的最小值.
的最小值.(1)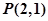 ;(2)①
;(2)①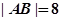 ;②
;②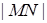 的最小值是
的最小值是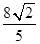 .
.
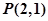 ;(2)①
;(2)①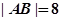 ;②
;②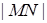 的最小值是
的最小值是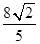 .
.试题分析:(1)数形结合,找出与
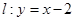 与平行的切线的切点即为P.(2)易得直线方程
与平行的切线的切点即为P.(2)易得直线方程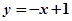 ,与抛物线联立,利用弦长公式,可求AB;②设
,与抛物线联立,利用弦长公式,可求AB;②设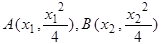 ,可得AO,BO方程,与抛物线联立
,可得AO,BO方程,与抛物线联立试题解析:
解:(1)设
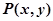 ,
,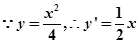 ,
,由题可知:

所求的点为:
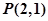 (或者用距离公式或
(或者用距离公式或 同样给分) 3分
同样给分) 3分(2)①易知直线AB:
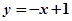 ,
,联立:
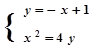 ,消去y得,
,消去y得,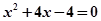 5分
5分设
 ,则
,则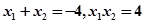
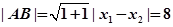 (用定义同样给分) 8分
(用定义同样给分) 8分②设
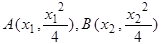 ,所以
,所以
所以
 的方程是:
的方程是: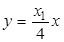 ,由
,由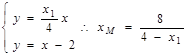 ,
,同理由
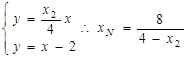 9分
9分所以

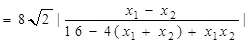 ① 10分
① 10分设
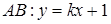 ,由
,由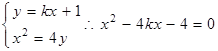 ,
,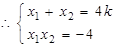 且
且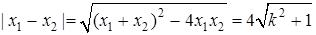 ,
,代入①得到:
 , 12分
, 12分设
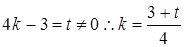 ,
,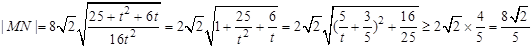 ,
,所以此时
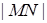 的最小值是
的最小值是 ,此时
,此时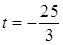 ,
,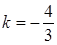 ; 13分
; 13分综上:
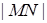 的最小值是
的最小值是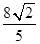 。 14分
。 14分
练习册系列答案
相关题目
 ,求点A的坐标;
,求点A的坐标; 上的动点,点P在y轴上的射影是M,点A 的坐标是(4,a),则当
上的动点,点P在y轴上的射影是M,点A 的坐标是(4,a),则当 时,
时, 的最小值是( )
的最小值是( )



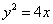 的焦点到双曲线
的焦点到双曲线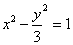 的渐近线的距离是( )
的渐近线的距离是( )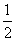

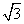
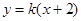 (k>0)与抛物线
(k>0)与抛物线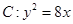 相交于A、B两点,
相交于A、B两点,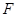 为
为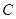 的焦点,若
的焦点,若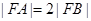 ,则k的值为()
,则k的值为()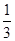
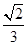
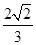
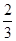
 上一点,设P到此抛物线准线的距离是
上一点,设P到此抛物线准线的距离是 ,到直线
,到直线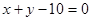 的距离是
的距离是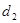 ,则
,则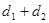 的最小值是
的最小值是 的焦点F作直线AB,CD与抛物线交于A、B、C、D四点,且
的焦点F作直线AB,CD与抛物线交于A、B、C、D四点,且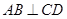 ,则
,则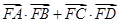 的最大等于 ( )
的最大等于 ( )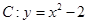 ,过原点的动直线
,过原点的动直线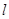 交抛物线
交抛物线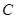 于
于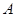 、
、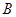 两点,
两点,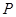 是
是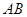 的中点,设动点
的中点,设动点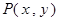 ,则
,则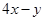 的最大值是( )
的最大值是( )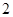
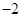
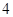
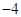
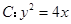 的焦点为
的焦点为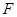 ,
,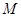 为抛物线
为抛物线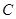 上一点,且点
上一点,且点 .
.