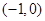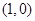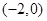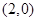题目内容
已知点P是抛物线 上一点,设P到此抛物线准线的距离是
上一点,设P到此抛物线准线的距离是 ,到直线
,到直线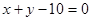 的距离是
的距离是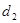 ,则
,则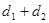 的最小值是
的最小值是
 上一点,设P到此抛物线准线的距离是
上一点,设P到此抛物线准线的距离是 ,到直线
,到直线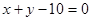 的距离是
的距离是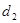 ,则
,则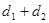 的最小值是
的最小值是6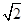
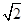
试题分析:∵抛物线方程是y2=-8x
∴抛物线的焦点为F(-2,0),准线方程是x=2
P是抛物线y2=-8x上一点,过P点作PQ与准线垂直,垂足为Q,
再过P作PM与直线x+y-10=0垂直,垂足为M
则PQ=d1,PM=d2
连接PF,根据抛物线的定义可得PF=PQ=d1,所以d1+d2=PF+PM,
可得当P、F、M三点共线且与直线x+y-10=0垂直时,dl+d2最小.(即图中的F、P0、M0位置)
∴dl+d2的最小值是焦点F到直线x+y-10=0的距离,
即
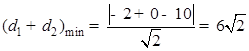 .
.
练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
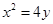 ,直线
,直线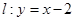 ,
,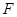 是抛物线的焦点。
是抛物线的焦点。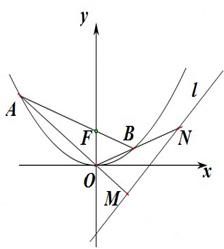
 ,使点
,使点 的距离最小;
的距离最小;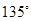 ,求弦AB的长度;
,求弦AB的长度;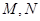 两点,求
两点,求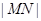 的最小值.
的最小值.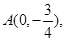 点
点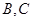 分别是
分别是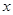 轴和
轴和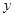 轴上的动点,且
轴上的动点,且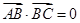 ,动点
,动点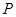 满足
满足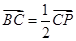 ,设动点
,设动点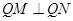 ,过M,N两点分别作曲线E的切线,记两切线的交点为
,过M,N两点分别作曲线E的切线,记两切线的交点为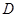 ,求
,求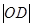 的最小值.
的最小值.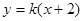 (k>0)与抛物线
(k>0)与抛物线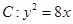 相交于
相交于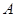 、
、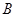 两点,
两点,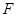 为
为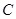 的焦点,若
的焦点,若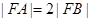 ,则k的值为 .
,则k的值为 .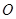 为坐标原点,
为坐标原点,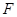 为抛物线
为抛物线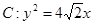 的焦点,
的焦点,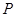 为
为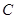 上一点,若
上一点,若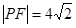 ,则△
,则△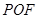 的面积为( )
的面积为( )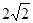
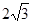
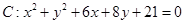 ,抛物线
,抛物线 的准线为L,设抛物线上任意一点
的准线为L,设抛物线上任意一点 到直线L的距离为
到直线L的距离为 ,则
,则 的最小值为
的最小值为
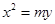

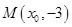 到焦点的距离为
到焦点的距离为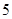 ,则实数
,则实数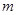 的值为( )
的值为( )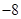

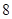
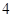
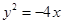 ,则它的焦点坐标为( )
,则它的焦点坐标为( )