题目内容
11.已知等差数列{an}的前n项和为Sn,且a2=$\frac{5}{3}$,S10=40.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=(-1)n+1anan+1(n∈N*),求数列{bn}的前2n项的和T2n.
分析 (Ⅰ)通过a2=$\frac{5}{3}$,S10=40计算即得结论;
(Ⅱ)通过bn=(-1)n+1anan+1(n∈N*)写出T2n的表达式,利用相邻两项的差为定值提取公因式计算即得结论.
解答 解:(Ⅰ)设等差数列{an}的公差为d,
则$\left\{\begin{array}{l}{{a}_{1}+d=\frac{5}{3}}\\{10{a}_{1}+\frac{10×9}{2}d=40}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}_{1}=1}\\{d=\frac{2}{3}}\end{array}\right.$,
故an=1+$\frac{2}{3}$(n-1)=$\frac{2}{3}$n+$\frac{1}{3}$;
(Ⅱ)T2n=a1a2-a2a3+a3a4-a4a5+…+a2na2n+1
=a2(a1-a3)+a4(a3-a5)+…+a2n(a2n-1a2n+1)
=-$\frac{4}{3}$(a2+a4+a6+…+a2n)
=-$\frac{4}{9}$(2n2+3n).
点评 本题考查求数列的通项、前n项和,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
1.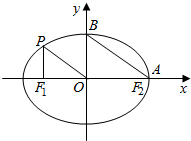 如图,从椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x 轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP,则椭圆的离心率为( )
如图,从椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x 轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP,则椭圆的离心率为( )
 如图,从椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x 轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP,则椭圆的离心率为( )
如图,从椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x 轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP,则椭圆的离心率为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
2.已知cosα=$\frac{3}{5}$,则sin($\frac{π}{2}$-α)=( )
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |
6.复数(1-4i)2的虚部为( )
| A. | -4i | B. | -4 | C. | -8i | D. | -8 |
16.对两个变量y和x进行回归分析,得到一组样本数据:(x1,y1),(x2,y2),…,(xn,yn),则下列说法中不正确的是( )
| A. | 由样本数据得到的回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$必过样本中心($\overline{x}$,$\overline{y}$) | |
| B. | 残差平方和越小的模型,拟合的效果越好 | |
| C. | 用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好 | |
| D. | 两个随机变量的线性相关性越强,相关系数的绝对值越接近于1 |
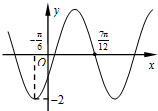 已知函数f(x)=2sin(ωx+θ ) (ω>0)的图象如图所示,则ω=2,若将函数f(x)的图象向左平移φ $({0<φ<\frac{π}{2}})$个单位后得到一个偶函数,则φ=$\frac{π}{3}$.
已知函数f(x)=2sin(ωx+θ ) (ω>0)的图象如图所示,则ω=2,若将函数f(x)的图象向左平移φ $({0<φ<\frac{π}{2}})$个单位后得到一个偶函数,则φ=$\frac{π}{3}$.