题目内容
13．已知命题P：不等式a2-4a+3＜0的解集；命题Q：使（a-2）x2+2（a-2）x-4＜0对任意实数x恒成立的实数a，若P∨Q是真命题，求实数a的取值范围．分析 据复合函数单调性的判定方法，我们可以判断出命题p满足时，参数a的取值范围，进而根据二次不等式恒成立的充要条件，我们易判断出命题q满足时，参数a的取值范围，进而根据p∨q是真命题，易得到满足条件的实数a的取值范围．
解答 解：不等式a2-4a+3＜0得，1＜a＜3，
所以命题为； 1＜a＜3，
由不等式（a-2）x2+2（a-2）x-4＜0对任意实数x恒成立；
得a
a=2 或$\left\{\begin{array}{l}a-2＜0\\△=4{（a-2）^2}+16（a-2）＜0\end{array}\right.$，
解得-2＜a≤2，
∵P∨Q是真命题，
∴a的取值范围是-2＜a＜3．
点评 本题考查的知识点是命题的真假判断与应用，函数恒成立问题，其中根据已知求出命题p和q满足时，参数a的取值范围，是解答本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
3．当双曲线C不是等轴双曲线时，我们把以双曲线C的实轴、虚轴的端点作为顶点的椭圆称为双曲线C的“伴生椭圆”．则离心率为$\sqrt{3}$的双曲线的“伴生椭圆”的离心率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{6}}}{3}$ | C． | $\frac{{\sqrt{3}}}{3}$ | D． | $\frac{{\sqrt{2}}}{2}$ |
4．已知a=0.80.2，b=0.80.5，c=5.20.1，则这三个数的大小关系为（ ）
| A． | b＜a＜c | B． | a＜b＜c | C． | c＜a＜b | D． | c＜b＜a |
1．
如图，从椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$上一点P向x轴作垂线，垂足恰为左焦点F1，又点A是椭圆与x 轴正半轴的交点，点B是椭圆与y轴正半轴的交点，且AB∥OP，则椭圆的离心率为（ ）
如图，从椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$上一点P向x轴作垂线，垂足恰为左焦点F1，又点A是椭圆与x 轴正半轴的交点，点B是椭圆与y轴正半轴的交点，且AB∥OP，则椭圆的离心率为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{5}}}{5}$ | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
8．在△ABC中，若C=90°，三边为a，b，c，则$\frac{a+b}{c}$的范围是（ ）
| A． | （$\sqrt{2}$，2） | B． | （1，$\sqrt{2}$] | C． | （0，$\sqrt{2}$] | D． | [$\frac{{\sqrt{2}}}{2}$，$\sqrt{2}$] |
18．函数y=f（x）的图象如图所示，则以下描述正确的是（ ）
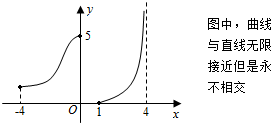
| A． | 函数f（x）的定义域为[-4，4） | |
| B． | 函数f（x）的值域为[0，5] | |
| C． | 此函数在定义域内既不是增函数也不是减函数 | |
| D． | 对于任意的y∈[0，+∞），都有唯一的自变量x与之对应 |
5．设全集U=R，已知集合M={x|x2-x＞0}，N={x|$\frac{x-1}{x}$＜0}，则有（ ）
| A． | M∪N=R | B． | M∩N=∅ | C． | CuN=M | D． | CvM⊆N |
2．已知cosα=$\frac{3}{5}$，则sin（$\frac{π}{2}$-α）=（ ）
| A． | $\frac{3}{5}$ | B． | -$\frac{3}{5}$ | C． | $\frac{4}{5}$ | D． | -$\frac{4}{5}$ |