题目内容
10．等比数列{an}的前n项和为Sn，S2n=4（a1+a3+…+a2n-1），a1a2a3=8，则a4=（ ）| A． | 2 | B． | 6 | C． | 18 | D． | 54 |
分析 先根据等比数列的性质可求出a2的值，然后根据S2n=4（a1+a3+…+a2n-1）中令n=1可求出首项a1，从而求出公比，即可求出a4的值．
解答 解：利用等比数列的性质可得，a1a2a3=a23=8 即a2=2，
因为S2n=4（a1+a3+…+a2n-1），
所以n=1时有，S2=a1+a2=4a1从而可得a1=$\frac{2}{3}$，q=3，
所以，a4=$\frac{2}{3}$×33=18，
故选；C．
点评 本题主要考查了等比数列的性质，等比数列的前 n项和公式及通项公式，属基础题．
练习册系列答案
出彩同步大试卷系列答案
相关题目
1．
如图，从椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$上一点P向x轴作垂线，垂足恰为左焦点F1，又点A是椭圆与x 轴正半轴的交点，点B是椭圆与y轴正半轴的交点，且AB∥OP，则椭圆的离心率为（ ）
如图，从椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$上一点P向x轴作垂线，垂足恰为左焦点F1，又点A是椭圆与x 轴正半轴的交点，点B是椭圆与y轴正半轴的交点，且AB∥OP，则椭圆的离心率为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{5}}}{5}$ | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
18．函数y=f（x）的图象如图所示，则以下描述正确的是（ ）
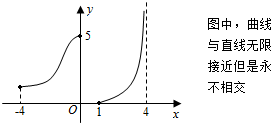
| A． | 函数f（x）的定义域为[-4，4） | |
| B． | 函数f（x）的值域为[0，5] | |
| C． | 此函数在定义域内既不是增函数也不是减函数 | |
| D． | 对于任意的y∈[0，+∞），都有唯一的自变量x与之对应 |
5．设全集U=R，已知集合M={x|x2-x＞0}，N={x|$\frac{x-1}{x}$＜0}，则有（ ）
| A． | M∪N=R | B． | M∩N=∅ | C． | CuN=M | D． | CvM⊆N |
2．已知cosα=$\frac{3}{5}$，则sin（$\frac{π}{2}$-α）=（ ）
| A． | $\frac{3}{5}$ | B． | -$\frac{3}{5}$ | C． | $\frac{4}{5}$ | D． | -$\frac{4}{5}$ |
已知函数f（x）=2sin（ωx+θ ） （ω＞0）的图象如图所示，则ω=2，若将函数f（x）的图象向左平移φ $（{0＜φ＜\frac{π}{2}}）$个单位后得到一个偶函数，则φ=$\frac{π}{3}$．