Question

【题目】下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.

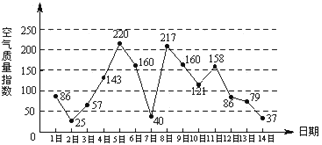
(Ⅰ)求此人到达当日空气重度污染的概率；

(Ⅱ)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望.

Answer 1

【答案】（1）

（2）X的分布列为：

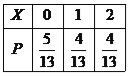
X的期望EX==．

【解析】

试题(I) 3月1日至3月13日中,只有5日与8日为重度污染，再根据古典概率的求法即可得到所求概率；(Ⅱ)先确定X可能的取值0、1、2共三种,然后根据图像分别计算X为0、1及2时的概率.即可得到分布列，从而求出期望.

试题解析：设表示事件“此人于3月i日到达该市”(i="1,2,..,13).

根据题意,,且.

(I)设B为事件“此人到达当日空气重度污染”,则,

所以.

(II)由题意可知,X的所有可能取值为0,1,2,且

P(X=1)=P(A3∪A6∪A7∪A11)= P(A3)+P(A6)+P(A7)+P(A11)=,

P(X=2)=P(A1∪A2∪A12∪A13)= P(A1)+P(A2)+P(A12)+P(A13)=,

P(X=0)=1-P(X=1)-P(X=2)=,

所以X的分布列为:

故X的期望.