题目内容
【题目】已知椭圆![]() :
:![]() 的左、右焦点为
的左、右焦点为![]() ,
,![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 面积的最大值为
面积的最大值为![]() ,周长为6.
,周长为6.
(1)求椭圆![]() 的方程,并求椭圆
的方程,并求椭圆![]() 的离心率;
的离心率;
(2)已知直线![]() :
:![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,若在
,若在![]() 轴上存在点
轴上存在点![]() ,使得
,使得![]() 与
与![]() 中点的连线与直线
中点的连线与直线![]() 垂直,求实数
垂直,求实数![]() 的取值范围
的取值范围
【答案】(1)![]() ,椭圆的离心率
,椭圆的离心率![]() (2)
(2)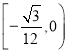
【解析】
(1)利用基本量法,列方程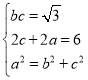 ,求解即可.
,求解即可.
(2)联立方程组,利用根与系数的关系求出![]() 的中点
的中点![]() 的坐标,根据
的坐标,根据![]() 与
与![]() 中点的连线与直线
中点的连线与直线![]() 垂直得出
垂直得出![]() 点横坐标
点横坐标![]() 的表达式,利用基本不等式得出
的表达式,利用基本不等式得出![]() 的取值范围.
的取值范围.
(1)由题意得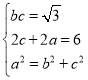 ,解之得
,解之得![]() ,
,![]() ,
,![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() ,
,
椭圆的离心率![]() ;
;
(2)由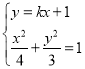 得
得![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
所以线段![]() 中点的坐标为
中点的坐标为![]() ,
,
则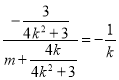 ,整理得
,整理得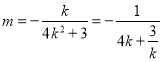 ,
,
因为![]() ,所以
,所以![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时上式取得等号,
时上式取得等号,
此时![]() 取得最小值
取得最小值![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以实数![]() 的取值范围是
的取值范围是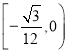 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】假设关于某设备的使用年限![]() (年)和所支出的年平均维修费用
(年)和所支出的年平均维修费用![]() (万元)(即维修费用之和除以使用年限),有如下的统计资料:
(万元)(即维修费用之和除以使用年限),有如下的统计资料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
维修费用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)画出散点图;
(2)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(3)估计使用年限为10年时所支出的年平均维修费用是多少?
参考公式: 






