题目内容
【题目】已知抛物线C:![]() (
(![]() )的准线与x轴交于点A,点
)的准线与x轴交于点A,点![]() 在抛物线C上.
在抛物线C上.
(1)求C的方程;
(2)过点M作直线l,交抛物线C于另一点N,若![]() 的面积为
的面积为![]() ,求直线l的方程
,求直线l的方程
【答案】(1)![]() ;(2)
;(2)![]() ,或
,或![]() .
.
【解析】
(1)将点![]() 代入抛物线的方程即可求出答案;
代入抛物线的方程即可求出答案;
(2)由(1)知,![]() ,
,![]() ,求得直线
,求得直线![]() 的方程为
的方程为![]() ,
,![]() ,设点
,设点 到直线
到直线![]() 的距离为
的距离为![]() ,根据三角形的面积公式及点到直线的距离公式可得
,根据三角形的面积公式及点到直线的距离公式可得 ,由此结合斜率计算公式及直线的点斜式方程即可求出答案.
,由此结合斜率计算公式及直线的点斜式方程即可求出答案.
解:(1)∵点![]() 在抛物线
在抛物线![]() 上,
上,
∴![]() ,∴
,∴![]() 或
或![]() (舍去),
(舍去),
∴抛物线C的方程为![]() ;
;
(2)由(1)知抛物线C的方程为![]() ,
,![]() ,
,![]() ,
,
![]() ,∴直线
,∴直线![]() 的方程为
的方程为![]() ,即
,即![]() ,且
,且![]() ,
,
∴点N到直线![]() 的距离
的距离 ,
,
设N点的坐标为 ,
,
则 ,
,
解得![]() 或
或![]() ,
,
即N点的坐标为![]() 或
或![]() ,
,
若取![]() ,则
,则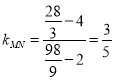 ,
,
直线l的方程为![]() ,即
,即![]() ,
,
若取![]() ,则
,则 ,
,
直线l的方程为![]() ,即
,即![]() ,
,
∴直线l的方程为![]() ,或
,或![]() .
.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目