题目内容
(本小题满分12分)
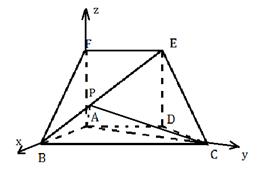
如图,正方形ADEF和等腰梯形ABCD垂直,已知BC=2AD=4,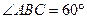 ,
,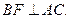

(I)求证: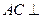 面ABF;
面ABF;
(II)求异面直线BE与AC所成的角的余弦值;
(III)在线段BE上是否存在一点P,使得平面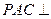 平面BCEF?若存在,求出
平面BCEF?若存在,求出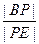 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。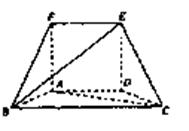
如图,正方形ADEF和等腰梯形ABCD垂直,已知BC=2AD=4,
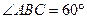 ,
,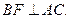

(I)求证:
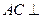 面ABF;
面ABF;(II)求异面直线BE与AC所成的角的余弦值;
(III)在线段BE上是否存在一点P,使得平面
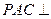 平面BCEF?若存在,求出
平面BCEF?若存在,求出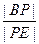 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
(1)略
(2)
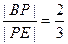
(3)
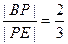
⑴证明:因为面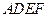
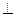 面
面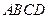 ,
,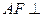 交线
交线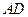 ,
,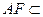 面
面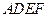 ,
,
所以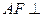 面
面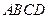 . 2分
. 2分
故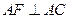 , 又
, 又 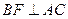 ,
, 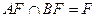 .
.
所以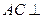 面
面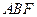 .……………4分
.……………4分
 (2)解:由⑴得
(2)解:由⑴得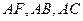 两两互相垂直,
两两互相垂直,
故可以以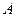 点为坐标原点,建立如图空间直角坐标系
点为坐标原点,建立如图空间直角坐标系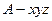 ,则
,则
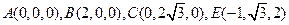 .
.
……………………………………6分
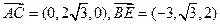 ,
,
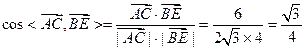 .
.
即异面直线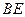 与
与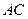 所成的角的余弦值为
所成的角的余弦值为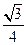 .……………………8分
.……………………8分
⑶解:若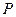 为线段
为线段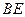 上的一点,且
上的一点,且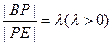 (点
(点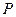 与点
与点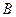 重合时不合题意),
重合时不合题意),
则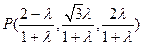 .………………………………9分
.………………………………9分
设平面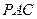 和平面
和平面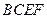 的法向量分别为
的法向量分别为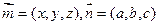 ,
,
由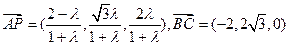 得,
得,
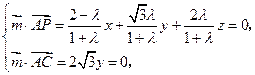 即
即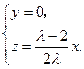
所以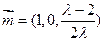 为平面
为平面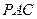 的一个法向量,
的一个法向量,
同理可求得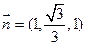 为平面
为平面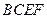 的一个法向量. ………… 11分
的一个法向量. ………… 11分
当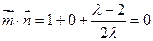 ,即
,即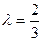 时平面
时平面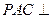 平面
平面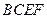 ,
,
故存在这样的点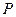 ,此时
,此时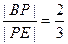 . ………………………………12分略
. ………………………………12分略
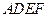
 面
面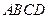 ,
,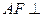 交线
交线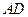 ,
,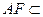 面
面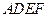 ,
, 所以
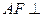 面
面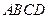 . 2分
. 2分故
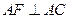 , 又
, 又 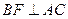 ,
, 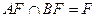 .
.所以
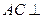 面
面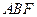 .……………4分
.……………4分 (2)解:由⑴得
(2)解:由⑴得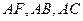 两两互相垂直,
两两互相垂直,故可以以
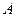 点为坐标原点,建立如图空间直角坐标系
点为坐标原点,建立如图空间直角坐标系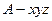 ,则
,则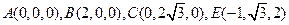 .
.……………………………………6分
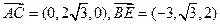 ,
,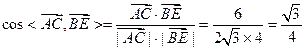 .
.即异面直线
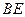 与
与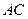 所成的角的余弦值为
所成的角的余弦值为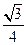 .……………………8分
.……………………8分⑶解:若
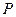 为线段
为线段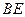 上的一点,且
上的一点,且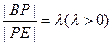 (点
(点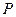 与点
与点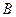 重合时不合题意),
重合时不合题意),则
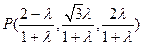 .………………………………9分
.………………………………9分设平面
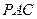 和平面
和平面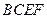 的法向量分别为
的法向量分别为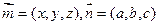 ,
,由
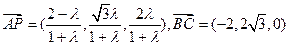 得,
得,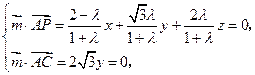 即
即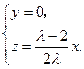
所以
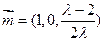 为平面
为平面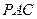 的一个法向量,
的一个法向量,同理可求得
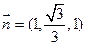 为平面
为平面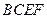 的一个法向量. ………… 11分
的一个法向量. ………… 11分当
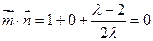 ,即
,即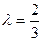 时平面
时平面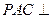 平面
平面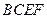 ,
,故存在这样的点
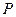 ,此时
,此时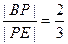 . ………………………………12分略
. ………………………………12分略
练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
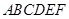 中,已知平面
中,已知平面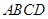 是边长为
是边长为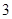 的正方形,
的正方形,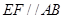 ,
,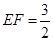 ,且
,且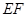 与平面
与平面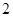 ,则该多面体的体积为( )
,则该多面体的体积为( )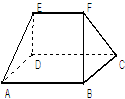
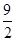
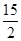
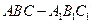 的底面
的底面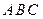 位于平行四边形
位于平行四边形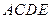 中,
中,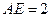 ,
,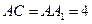 ,
,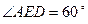 ,点
,点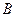 为
为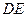 中点.
中点. 
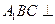 平面
平面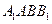 .
. 面角
面角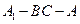 的大小为
的大小为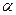 ,直线
,直线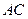 与平面
与平面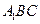 所成的角为
所成的角为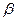 ,求
,求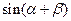 的值.
的值.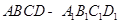 中,
中,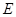 ,
,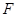 分别为 棱
分别为 棱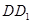 ,
,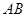 上的点. 已知下列判断:
上的点. 已知下列判断: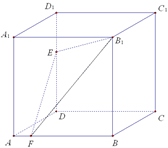
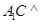 平面
平面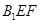 ;②
;②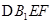 在侧面
在侧面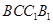 上 的正投影是面积为定值的三角形;③在平面
上 的正投影是面积为定值的三角形;③在平面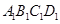 内总存在与平面
内总存在与平面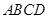 所成的二面角(锐角)的大小与点
所成的二面角(锐角)的大小与点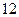 分)在边长为
分)在边长为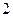 的正方体
的正方体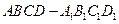 中,
中,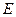 是
是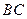 的中点,
的中点,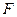 是
是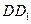 的中点,
的中点, 求证:
求证: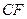 ∥
∥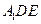 ;
;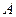 到平面
到平面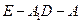 的平面角大小的余弦值.
的平面角大小的余弦值.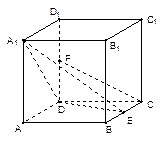
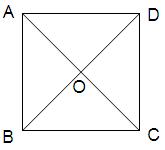
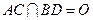 .将正方形ABCD沿对角线
.将正方形ABCD沿对角线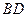 折起,使
折起,使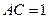 ,得到三棱锥A—BCD,如图所示.
,得到三棱锥A—BCD,如图所示.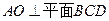 ;
;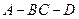 的余弦值.
的余弦值.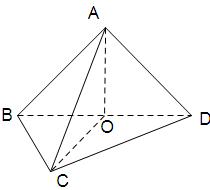
 ,AB=BC=1。M为PC的中点。
,AB=BC=1。M为PC的中点。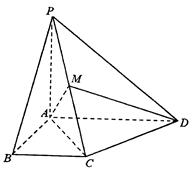
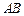 为圆
为圆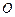 的直径,点
的直径,点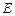 、
、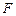 在圆
在圆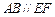 ,矩形
,矩形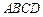 所在的平面和圆
所在的平面和圆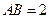 ,
, 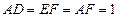 .
.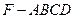 的体积
的体积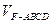 ;(Ⅱ)求证:平面
;(Ⅱ)求证:平面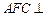 平面
平面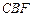 ;
;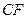 上是否存在一点
上是否存在一点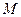 ,使得
,使得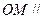 平面
平面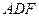 ,并说明理由.
,并说明理由.
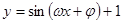 的一段图象如图所示,则它的一个周期T、初相
的一段图象如图所示,则它的一个周期T、初相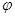 依次为( )
依次为( )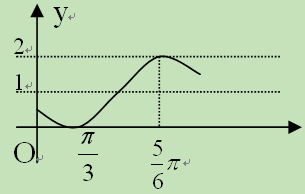
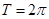 ,
,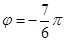
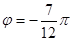
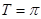 ,
,