题目内容
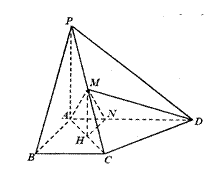
(12分)如图,在四棱锥P—ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD//BC且AD﹥BC,∠DAB=∠ABC=90°,PA=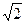 ,AB=BC=1。M为PC的中点。
,AB=BC=1。M为PC的中点。
(1)求二面角M—AD—C的大小;(6分)
(2)如果∠AMD=90°,求线段AD的长。(6分)
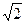 ,AB=BC=1。M为PC的中点。
,AB=BC=1。M为PC的中点。
(1)求二面角M—AD—C的大小;(6分)
(2)如果∠AMD=90°,求线段AD的长。(6分)
(1)
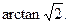
(2)2
(1)取AC的中点H,连MH,则MH//PA,所以MH⊥平面ABCD,过H作HN⊥AD于N,连MN,由三垂线定理可得MN⊥AD,则∠MNH就为所求的二面角的平面角
AH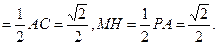
在Rt△ANH中,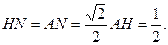
则在Rt△MHN中,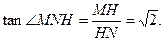
故所示二面角的大小为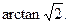
(2)若AM⊥MD,又因为PA=AC=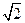 ,M为PC的中点,
,M为PC的中点,
则AM⊥PC,所以AM⊥平面PCD,则AM⊥CD。
AM在平面ABCD的射影为CD,由三垂线定理可知其等价于AC⊥CD,
此时△ACD为等腰直角三角形,所以AD=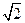 AC=2
AC=2

AH
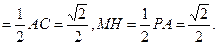
在Rt△ANH中,
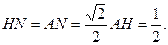
则在Rt△MHN中,
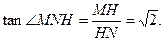
故所示二面角的大小为
(2)若AM⊥MD,又因为PA=AC=
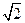 ,M为PC的中点,
,M为PC的中点,则AM⊥PC,所以AM⊥平面PCD,则AM⊥CD。
AM在平面ABCD的射影为CD,由三垂线定理可知其等价于AC⊥CD,
此时△ACD为等腰直角三角形,所以AD=
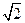 AC=2
AC=2
练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 为
为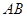 的中点,
的中点,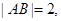
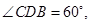
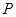 为
为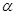 内的动点,且
内的动点,且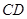 的距离为
的距离为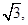 则
则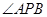 的最大值为
的最大值为 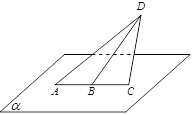
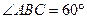 ,
,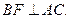

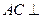 面ABF;
面ABF;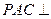 平面BCEF?若存在,求出
平面BCEF?若存在,求出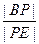 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。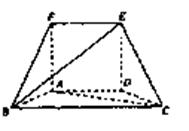
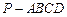
 中,
中,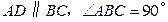 ,
, .
.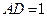 ,
,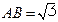 ,
,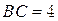 .
.
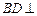
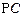 ;
;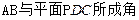 ;
;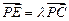 ,若
,若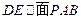 ,求
,求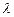 的值。
的值。 中,P是侧棱
中,P是侧棱 上的一点,
上的一点, .
.  时,求直线AP与平面BDD1B1所成角的度数;
时,求直线AP与平面BDD1B1所成角的度数; 上是否存在一个定点
上是否存在一个定点 ,使得对任意的m,
,使得对任意的m, ⊥AP,并证明你的结论.
⊥AP,并证明你的结论. 
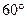 .且点E在平面ABC上的射影落在
.且点E在平面ABC上的射影落在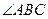 的平分线上。
的平分线上。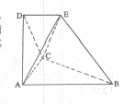
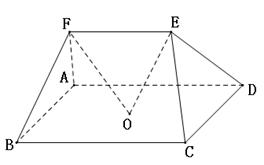
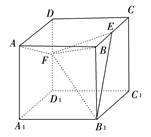
 ,则α⊥β
,则α⊥β 中,点
中,点 是矩形
是矩形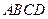 的对角线的交点,三角形
的对角线的交点,三角形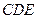 是等边三角形,棱
是等边三角形,棱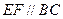 且
且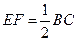 .
.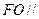 平面
平面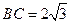 ,
,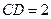 ,
,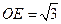 ,
,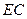 与平面
与平面