题目内容
(本小题满分12分)
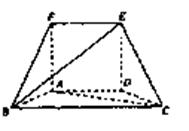
如图,直三棱柱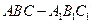 的底面
的底面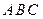 位于平行四边形
位于平行四边形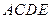 中,
中,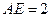 ,
,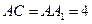 ,
,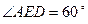 ,点
,点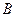 为
为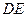 中点.
中点.

(1)求证:平面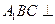 平面
平面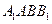 .
.
(2)设二 面角
面角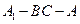 的大小为
的大小为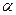 ,直线
,直线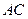 与平面
与平面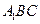 所成的角为
所成的角为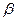 ,求
,求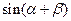 的值.
的值.
如图,直三棱柱
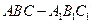 的底面
的底面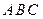 位于平行四边形
位于平行四边形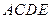 中,
中,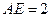 ,
,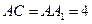 ,
,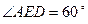 ,点
,点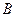 为
为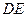 中点.
中点. 
(1)求证:平面
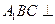 平面
平面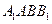 .
.(2)设二
 面角
面角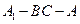 的大小为
的大小为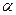 ,直线
,直线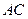 与平面
与平面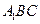 所成的角为
所成的角为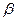 ,求
,求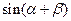 的值.
的值.(1)略
(2)
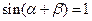
证明:(Ⅰ)∵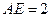 ,
,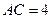 ,
,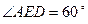 ,点
,点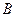 为
为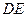 中点.
中点.
∴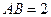 ,
,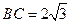 ,
,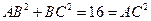 ,∴
,∴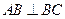 .
.
又 面
面 ,
,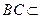 面
面 ,∴
,∴ ,
,
 而
而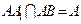 ,∴
,∴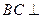 平面
平面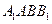
∵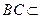 平面
平面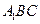 ,∴平面
,∴平面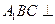 平面
平面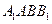 .
.
(Ⅱ)由(Ⅰ)可知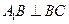 ,
,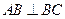
∴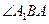 为二面角
为二面角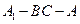 的平面角,即
的平面角,即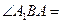
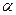 ,
,
在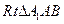 中,
中,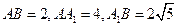 ,
,
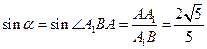 ,
,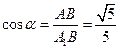 .
.
以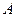 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系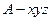 如图所示,
如图所示,
其中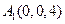 ,
,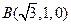 ,
,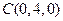 ,
,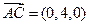 ,
,
 ,
,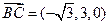 ,设
,设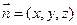 为平面
为平面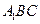 的一个法向量,则
的一个法向量,则
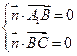 ,∴
,∴
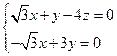 即
即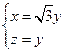
令 ,得平面
,得平面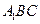 的一个法向量
的一个法向量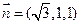 ,则
,则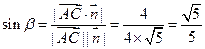 ,
,
又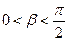 , ∴
, ∴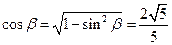 ,
,
∴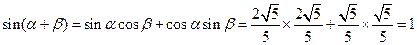 ,
,
即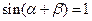 .
.
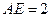 ,
,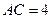 ,
,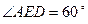 ,点
,点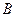 为
为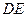 中点.
中点.∴
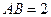 ,
,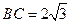 ,
,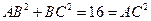 ,∴
,∴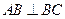 .
. 又
 面
面 ,
,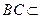 面
面 ,∴
,∴ ,
, 而
而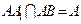 ,∴
,∴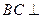 平面
平面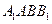
∵
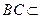 平面
平面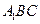 ,∴平面
,∴平面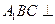 平面
平面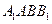 .
. (Ⅱ)由(Ⅰ)可知
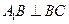 ,
,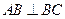
∴
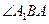 为二面角
为二面角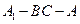 的平面角,即
的平面角,即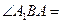
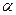 ,
,在
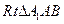 中,
中,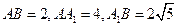 ,
,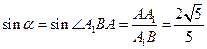 ,
,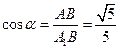 .
. 以
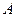 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系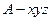 如图所示,
如图所示,其中
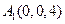 ,
,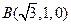 ,
,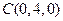 ,
,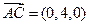 ,
, ,
,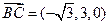 ,设
,设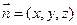 为平面
为平面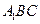 的一个法向量,则
的一个法向量,则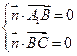 ,∴
,∴
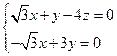 即
即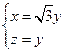
令
 ,得平面
,得平面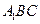 的一个法向量
的一个法向量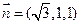 ,则
,则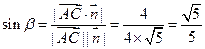 ,
, 又
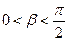 , ∴
, ∴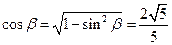 ,
, ∴
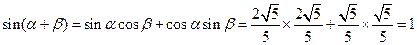 ,
, 即
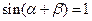 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 为
为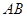 的中点,
的中点,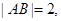
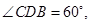
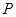 为
为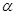 内的动点,且
内的动点,且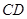 的距离为
的距离为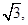 则
则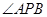 的最大值为
的最大值为 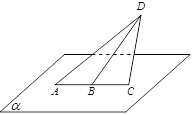
 中,
中,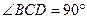 ,
,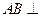 平面
平面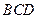 ,
,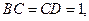
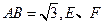 分别为
分别为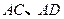 的中点.
的中点.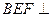 平面
平面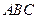 ;
;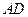 与平面
与平面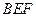 所成角的正弦值.
所成角的正弦值.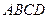 中,
中,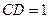 ,
,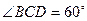 ,且
,且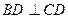 ,正方形
,正方形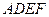 所在平面和平面
所在平面和平面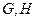 分别是
分别是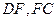 的中点.
的中点.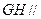 平面
平面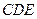 ;
;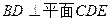 ;
;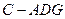 的体积.
的体积.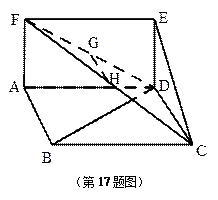
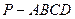 中,底面
中,底面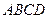 是直角梯形,
是直角梯形,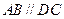 ,
,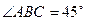 ,
,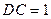 ,
,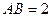 ,
,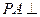 平面
平面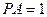 .
. 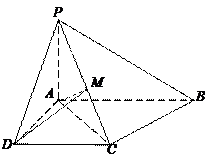
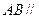 平面
平面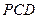 ;
;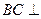 平面
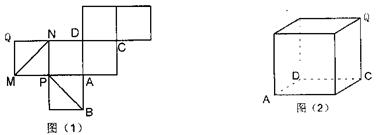
平面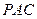 ;
;
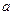 的正方体ABCD-A1B1C1D1中
的正方体ABCD-A1B1C1D1中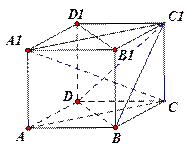
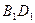 ∥平面C1BD
∥平面C1BD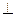 平面C1BD
平面C1BD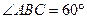 ,
,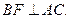

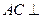 面ABF;
面ABF;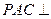 平面BCEF?若存在,求出
平面BCEF?若存在,求出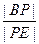 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。