题目内容
12.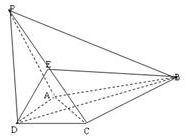 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.(1)证明:PA∥平面BDE;
(2)证明:AC⊥PB;
(3)求三棱锥E-ABD的体积.
分析 (1)设AC∩BD=F,连接EF,F为AC的中点,从而PA∥EF,由此能证明PA∥平面BDE.
(2)由等腰三角形性质得AC⊥BD,由线面垂直得PD⊥AC,由此能证明AC⊥平面PBD.
(3)由VB-ADE=VE-ABD,利用等积法能求出三棱锥B-ADE的体积.
解答 (1)证明:如图,设AC∩BD=F,连接EF,
∵AD=CD,且DB平分∠ADC,
∴F为AC的中点,
又∵E为PC的中点,∴EF为△PAC的中位线,
∴PA∥EF,
又∵EF?平面BDE,PA?平面BDE,
∴PA∥平面BDE.
(2)证明:∵AD=CD,且DB平分∠ADC,
∴AC⊥BD,
又PD⊥平面ABCD,AC?平面ABCD,
∴PD⊥AC,
又∵PD∩BD=D,且PD?平面PBD、BD?平面PBD,
∴AC⊥平面PBD.
(3)解:∵AD⊥CD,AD=CD=1,∴AC=$\sqrt{2}$,
由(1)知F为AC中点,∴AF=$\frac{\sqrt{2}}{2}$,
由(2)知AF⊥BD,∴S△ABD=$\frac{1}{2}×2\sqrt{2}×\frac{\sqrt{2}}{2}$=1,
又∵PD⊥平面ABCD,PD=2,E为PC中点,
∴E到平面ABD的距离为h=$\frac{1}{2}$PD=1,
∴VB-ADE=VE-ABD=$\frac{1}{3}{S}_{△ABD}•h$=$\frac{1}{3}$,
∴三棱锥B-ADE的体积为$\frac{1}{3}$.
点评 本题考查线面垂直、线面平行的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系和性质的合理运用.

练习册系列答案
相关题目
20.设函数f(x)=x2+ax,a∈R,则( )
| A. | 存在实数a,使f(x)为偶函数 | |
| B. | 存在实数a,使f(x)为奇函数 | |
| C. | 对于任意实数a,f(x)在(0,+∞)上单调递增 | |
| D. | 对于任意实数a,f(x)在(0,+∞)上单调递减 |
6.将函数f(x)=sin(2x-$\frac{π}{3}$)的图象上各点的横坐标压缩到原来的$\frac{1}{2}$,再将图象向左平移$\frac{π}{3}$个单位,那么所得到的图象的解析表达式为( )
| A. | y=sin(4x+$\frac{π}{3}$) | B. | y=sin(x-$\frac{2π}{3}$) | C. | y=sin4x | D. | y=-sin4x |