题目内容
4.已知函数f(x)=(m•2x+2-x)cosx(x∈R)是奇函数,则实数m=-1.分析 由f(x)为奇函数,便有f(-x)=-f(x),从而可以得到m+1=-(m+1)•22x,由于22x>0,从而m+1=0,这便求得m的值.
解答 解:f(x)是奇函数;
∴f(-x)=-f(x);
∴(m•2-x+2x)cosx=-(m•2x+2-x)cosx;
∴m•2-x+2x=-m•2x-2-x;
∴m+1=-(m+1)•22x;
∴m+1=0;
∴m=-1.
故答案为:-1.
点评 考查奇函数的定义,以及指数函数的值域,指数的运算.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
9.某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
其中:“积极参加班级工作且学习积极性高的学生”的频率为0.36.
(1)补全表中数据,并求“不太主动参加班级的学生”的频率;
(2)试运用独立性检验的思想方法分析:能否在犯错误概率不超过0.001的前提下认为,学生的学习积极性与对待班级工作的态度有关系?
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,(其中n=a+b+c+d)
临界值表:
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | 25 | ||
| 学习积极性一般 | 25 | ||
| 合计 | 24 | 26 | 50 |
(1)补全表中数据,并求“不太主动参加班级的学生”的频率;
(2)试运用独立性检验的思想方法分析:能否在犯错误概率不超过0.001的前提下认为,学生的学习积极性与对待班级工作的态度有关系?
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,(其中n=a+b+c+d)
临界值表:
| P(K2≥K0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
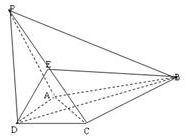 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.