题目内容
7.设复数Z=lg(m2-2m-2)+(m2-m-2)i,试求实数m取何值时(1)Z是实数;
(2)Z是纯虚数.
分析 (1)只要保证对数有意义并且虚部为0即可;
(2)只要实部为0,虚部不为0即可.
解答 解:由Z是实数,所以$\left\{\begin{array}{l}{{m}^{2}-2m-2>0}\\{{m}^{2}-m-2=0}\end{array}\right.$,解得m=-1;…(6分)
(2)Z是纯虚数,所以$\left\{\begin{array}{l}{{m}^{2}-2m-2=1}\\{{m}^{2}-m-2≠0}\end{array}\right.$,解得m=3.…(12分)
点评 本题考查了复数的基本概念;属于基础题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
18.已知向量$\overrightarrow a$=(2,-3),$\overrightarrow b$=(-5,8),则($\overrightarrow a$+$\overrightarrow b$)•$\overrightarrow b$等于( )
| A. | -34 | B. | 34 | C. | 55 | D. | -55 |
15.下列向量的运算中,正确的是( )
| A. | $\overrightarrow{AB}+\overrightarrow{BA}=2\overrightarrow{AB}$ | B. | $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{CA}$ | C. | $\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}$ | D. | $\overrightarrow{AB}-\overrightarrow{AD}-\overrightarrow{DC}=\overrightarrow{BC}$ |
12.在数列{an}中,如果存在非零常数T,使得am+T=am对于任意的非零自然数 均成立,那么就称数列{an}为周期数列,其中T 叫数列{an}的周期.已知数列{xn}满足xn+1=|xn-xn-1|(n≥2),如果x1=1,x2=a(a∈R,a≠0),当数列{xn}的周期最小时,该数列前2012项的和是( )
| A. | 670 | B. | 671 | C. | 1341 | D. | 1342 |
17.在△ABC中,若$\frac{a}{cosA}=\frac{b}{cosB}=\frac{c}{cosC}$,则△ABC的形状是( )
| A. | 等边三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 钝角三角形 |
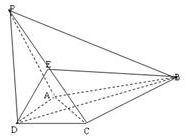 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.