题目内容
20.设函数f(x)=x2+ax,a∈R,则( )| A. | 存在实数a,使f(x)为偶函数 | |
| B. | 存在实数a,使f(x)为奇函数 | |
| C. | 对于任意实数a,f(x)在(0,+∞)上单调递增 | |
| D. | 对于任意实数a,f(x)在(0,+∞)上单调递减 |
分析 根据偶函数、奇函数的定义,二次函数的单调性即可判断每个选项的正误.
解答 解:A.a=0时,f(x)=x2为偶函数,∴该选项正确;
B.若f(x)为奇函数,f(-x)=x2-ax=-x2-ax;
∴x2=0,x≠0时显然不成立;
∴该选项错误;
C.f(x)的对称轴为x=$-\frac{a}{2}$;
当a<0时,f(x)在(0,+∞)没有单调性,∴该选项错误;
D.根据上面a<0时,f(x)在(0,+∞)上没有单调性,∴该选项错误.
故选A.
点评 考查偶函数、奇函数的定义,以及二次函数单调性的判断方法.

练习册系列答案
相关题目
8.设集合M={0,1,2},N={-1,0,1},则M∩N=( )
| A. | Φ | B. | {0,1} | C. | {0,1,2} | D. | {-1,0,1,2} |
5. 下表是随机抽取的某市五个地段五种不同户型新电梯房面积x(单位:十平方米)和相应的房价y(单位:万元)统计表:
下表是随机抽取的某市五个地段五种不同户型新电梯房面积x(单位:十平方米)和相应的房价y(单位:万元)统计表:
(Ⅰ)在给定的坐标系中画出散点图;
(Ⅱ)求用最小二乘法得到的回归直线方程(参考公式和数据:$\widehat{y}$=$\frac{\underset{\stackrel{n}{∑}}{i=1}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\underset{\stackrel{n}{∑}}{i=1}{x}_{i}^{2}-n•{\overline{x}}^{2}}$,$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,$\underset{\stackrel{5}{∑}}{i=1}$xiyi=4010);
(Ⅲ)请估计该市一面积为120m2的新电梯房的房价.
 下表是随机抽取的某市五个地段五种不同户型新电梯房面积x(单位:十平方米)和相应的房价y(单位:万元)统计表:
下表是随机抽取的某市五个地段五种不同户型新电梯房面积x(单位:十平方米)和相应的房价y(单位:万元)统计表:| x | 7 | 9 | 10 | 11 | 13 |
| y | 40 | 75 | 70 | 90 | 105 |
(Ⅱ)求用最小二乘法得到的回归直线方程(参考公式和数据:$\widehat{y}$=$\frac{\underset{\stackrel{n}{∑}}{i=1}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\underset{\stackrel{n}{∑}}{i=1}{x}_{i}^{2}-n•{\overline{x}}^{2}}$,$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,$\underset{\stackrel{5}{∑}}{i=1}$xiyi=4010);
(Ⅲ)请估计该市一面积为120m2的新电梯房的房价.
9.某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
其中:“积极参加班级工作且学习积极性高的学生”的频率为0.36.
(1)补全表中数据,并求“不太主动参加班级的学生”的频率;
(2)试运用独立性检验的思想方法分析:能否在犯错误概率不超过0.001的前提下认为,学生的学习积极性与对待班级工作的态度有关系?
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,(其中n=a+b+c+d)
临界值表:
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | 25 | ||
| 学习积极性一般 | 25 | ||
| 合计 | 24 | 26 | 50 |
(1)补全表中数据,并求“不太主动参加班级的学生”的频率;
(2)试运用独立性检验的思想方法分析:能否在犯错误概率不超过0.001的前提下认为,学生的学习积极性与对待班级工作的态度有关系?
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,(其中n=a+b+c+d)
临界值表:
| P(K2≥K0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
15.下列向量的运算中,正确的是( )
| A. | $\overrightarrow{AB}+\overrightarrow{BA}=2\overrightarrow{AB}$ | B. | $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{CA}$ | C. | $\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}$ | D. | $\overrightarrow{AB}-\overrightarrow{AD}-\overrightarrow{DC}=\overrightarrow{BC}$ |
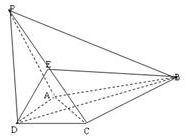 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.