题目内容
6.将函数f(x)=sin(2x-$\frac{π}{3}$)的图象上各点的横坐标压缩到原来的$\frac{1}{2}$,再将图象向左平移$\frac{π}{3}$个单位,那么所得到的图象的解析表达式为( )| A. | y=sin(4x+$\frac{π}{3}$) | B. | y=sin(x-$\frac{2π}{3}$) | C. | y=sin4x | D. | y=-sin4x |
分析 由条件利用函数y=Asin(ωx+φ)的图象变换规律、诱导公式,可得结论.
解答 解:将函数f(x)=sin(2x-$\frac{π}{3}$)的图象上各点的横坐标压缩到原来的$\frac{1}{2}$,可得y=sin(4x-$\frac{π}{3}$)的图象;
再将图象向左平移$\frac{π}{3}$个单位,那么所得到的图象的解析表达式y=sin[4(x+$\frac{π}{3}$)-$\frac{π}{3}$]=sin(4x+π)=-sin4x,
故选:D.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,诱导公式,属于基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
9.某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
其中:“积极参加班级工作且学习积极性高的学生”的频率为0.36.
(1)补全表中数据,并求“不太主动参加班级的学生”的频率;
(2)试运用独立性检验的思想方法分析:能否在犯错误概率不超过0.001的前提下认为,学生的学习积极性与对待班级工作的态度有关系?
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,(其中n=a+b+c+d)
临界值表:
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | 25 | ||
| 学习积极性一般 | 25 | ||
| 合计 | 24 | 26 | 50 |
(1)补全表中数据,并求“不太主动参加班级的学生”的频率;
(2)试运用独立性检验的思想方法分析:能否在犯错误概率不超过0.001的前提下认为,学生的学习积极性与对待班级工作的态度有关系?
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,(其中n=a+b+c+d)
临界值表:
| P(K2≥K0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
11.用反证法证明命题“a,b∈N,如果ab可被5整除,那么a,b至少有1个能被5整除.则假设的内容是( )
| A. | a,b都能被5整除 | B. | a,b有1个不能被5整除 | ||
| C. | a不能被5整除 | D. | a,b都不能被5整除 |
18.已知向量$\overrightarrow a$=(2,-3),$\overrightarrow b$=(-5,8),则($\overrightarrow a$+$\overrightarrow b$)•$\overrightarrow b$等于( )
| A. | -34 | B. | 34 | C. | 55 | D. | -55 |
15.下列向量的运算中,正确的是( )
| A. | $\overrightarrow{AB}+\overrightarrow{BA}=2\overrightarrow{AB}$ | B. | $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{CA}$ | C. | $\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}$ | D. | $\overrightarrow{AB}-\overrightarrow{AD}-\overrightarrow{DC}=\overrightarrow{BC}$ |
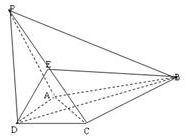 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.