题目内容
【题目】如图,网格纸上的小正方形边长为1,粗线画出的是某几何体的三视图,则该几何体外接球的体积为 . 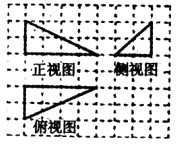
【答案】8 ![]() π
π
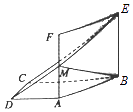
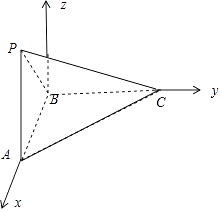
【解析】解:几何体为三棱锥,直观图如图所示:
其中PA⊥底面ABC,AB⊥BC,BC=4,AB=PA=2,
以B为原点建立如图所示的空间坐标系B﹣xyz,
则A=(2,0,0),B(0,0,0),C(0,4,0),P(2,0,2),
设棱锥的外接球球心为M(x,y,z),则MA=MB=MC=MP,
即(x﹣2)2+y2+z2=x2+y2+z2=x2+(y﹣4)2+z2=(x﹣2)2+y2+(z﹣2)2,
∴x=1,y=2,z=1,
∴外接球半径R=|MB|= ![]() =
= ![]() .
.
∴外接球的体积V= ![]() =8
=8 ![]() π.
π.
故答案为:8 ![]() π.
π.
作出几何体的直观图,建立坐标系,利用距离公式列方程求出外接球的球心坐标,从而得出外接球的半径,代入体积公式计算得出答案.

练习册系列答案
相关题目