题目内容
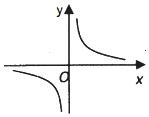
【题目】函数f（x）=
是定义在R上的奇函数，且f（1）=1．
（1）求a，b的值；
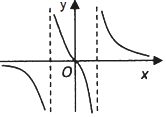
（2）判断并用定义证明f（x）在（
+∞）的单调性．
【答案】（1）a=5，b=0； （2）见解析.
【解析】
（1）根据函数为奇函数，可利用f（1）=1和f（-1）=-1，解方程组可得a、b值，然后进行验证即可；（2）根据函数单调性定义利用作差法进行证明．
（1）根据题意，f（x）=
是定义在R上的奇函数，且f（1）=1，
则f（-1）=-f（1）=-1，
则有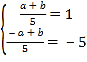
，解可得a=5，b=0；经检验，满足题意.
（2）由（1）的结论，f（x）=
，
设
＜x1＜x2，
f（x1）-f（x2）=
-
=
，
又由＜x1＜x2，则（1-4x1x2）＜0，（x1-x2）＜0，
则f（x1）-f（x2）＞0，
则函数f（x）在（，+∞）上单调递减．
【题目】为调查了解某省属师范大学师范类毕业生参加工作后，从事的工作与教育是否有关的情况，该校随机调查了该校80位性别不同的2016年师范类毕业大学生，得到具体数据如表：
与教育有关 | 与教育无关 | 合计 | |
男 | 30 | 10 | 40 |
女 | 35 | 5 | 40 |
合计 | 65 | 15 | 80 |
（1）能否在犯错误的概率不超过5%的前提下，认为“师范类毕业生从事与教育有关的工作与性别有关”？ 参考公式： 
（n=a+b+c+d）．
附表：
P（K2≥k0） | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.023 | 6.635 |
（2）求这80位师范类毕业生从事与教育有关工作的频率；
（3）以（2）中的频率作为概率．该校近几年毕业的2000名师范类大学生中随机选取4名，记这4名毕业生从事与教育有关的人数为X，求X的数学期望E（X）．
【题目】某单位附近只有甲，乙两个临时停车场，它们各有50个车位，为了方便市民停车，某互联网停车公司对这两个停车场在工作日某些固定时刻的剩余停车位进行记录，如下表：
时间 | 8点 | 10点 | 12点 | 14点 | 16点 | 18点 |
停车场甲 | 10 | 3 | 12 | 6 | 12 | 17 |
停车场乙 | 13 | 4 | 3 | 2 | 6 | 19 |
如果表中某一时刻停车场剩余停车位数低于总车位数的10%，那么当车主驱车抵达单位附近时，该公司将会向车主发出停车场饱和警报．
（Ⅰ）假设某车主在以上六个时刻抵达单位附近的可能性相同，求他收到甲停车场饱和警报的概率；
（Ⅱ）从这六个时刻中任选一个时刻，求甲停车场比乙停车场剩余车位数少的概率；
（Ⅲ）当停车场乙发出饱和警报时，求停车场甲也发出饱和警报的概率．
