Question

【题目】已知过抛物线E：x2=2py（p＞0）焦点F且倾斜角的60°直线l与抛物线E交于点M，N，△OMN的面积为4．
（1）求抛物线E的方程；
（2）设P是直线y=﹣2上的一个动点，过P作抛物线E的切线，切点分别为A、B，直线AB与直线OP、y轴的交点分别为Q、R，点C、D是以R为圆心、RQ为半径的圆上任意两点，求∠CPD最大时点P的坐标．

Answer 1

【答案】
（1）解：依题意， ，所以直线l的方程为 ；

由 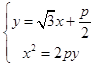得： ，

法一：所以 ，

O到MN的距离 ，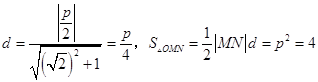

∴p=2，抛物线方程为x2=4y；

法二： ， ，故抛物线方程为x2=4y．

（2）解：设 ，由x2=4y得 ，

则切线PA方程为 即 ，

同理，切线PB方程为 ，

把P代入可得 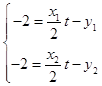，故直线AB的方程为 即tx﹣2y+4=0，

∴R（0，2）由 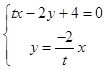得 ，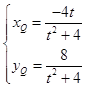

∴ ，

当PC，PD与圆R相切时角∠CPD最大，

此时 ，等号当 时成立，

∴当 时，所求的角∠CPD最大．

综上，当∠CPD最大时点P的坐标为 ．

法二：同解法一，得AB：tx﹣2y+4=0，注意到OP⊥AB，

∴ ，

∴

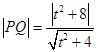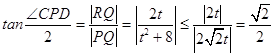
当且仅当t2+8即 时等号成立．

【解析】（1）利用点斜法写出直线l的方程为 ；结合△OMN的几何意义和三角形的面积求法求得p的值即可；（2）设 ，由x2=4y得 ，易得切线PA、PB的直线方程，把点P的坐标代入得到直线AB的方程tx﹣2y+4=0，由R的坐标和圆半径的计算方法求得半径的长度，则当PC，PD与圆R相切时角∠CPD最大，所以利用锐角三角函数的定义和不等式的基本性质进行解答即可．