题目内容
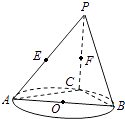
【题目】如图所示,在直角梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD=2DC,四边形ABEF是正方形,且平面ABEF⊥平面ABCD,M为AF的中点, (I)求证:AC⊥BM;
(II)求异面直线CE与BM所成角的余弦值.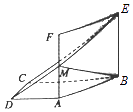
【答案】解:(I)证明:∵四边形ABEF为正方形,∴BE⊥AB.
∵平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,BE平面ABEF.
∴BE⊥平面ABCD.
∵AC平面ABCD,∴BE⊥AC.
设AD=1,则 ![]() ,
,
∴AC⊥AB且AB∩BE=B,
∴AC⊥平面ABEF,又BM平面ABEF.∴AC⊥BM.
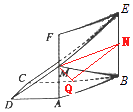
(II)取BC的中点记为Q,BE的中点记为N,连接MN,QN,DQ,
易得 ![]() .
.
在直角梯形ABCD中,由BC=2AD=2DC,
可得 ![]() ,
,
∴四边形DMNQ为平行四边形,
可得DM∥QN.
故DM∥CE,
那么∠DMB即为异面直线CE与BM所成的角(或其补角)
设BC=2a,则AD=DC=a,
可得 ![]() .
. 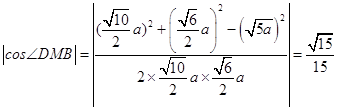 .
.
得异面直线CE与BM所成角的余弦值为 ![]() .
.
【解析】(I)线线垂直转化为线面垂直,要证明AC⊥BM;只需证明BE⊥平面ABCD,即可.(II)取BC的中点记为Q,BE的中点记为N,连接MN,QN,DQ,易得 ![]() .在直角梯形ABCD中,由BC=2AD=2DC可得
.在直角梯形ABCD中,由BC=2AD=2DC可得 ![]() ,所以四边形DMNQ为平行四边形,可得DM∥QN.故DM∥CE,∠DMB即为异面直线CE与BM所成的角(或其补角),利用余弦定理求解即可.
,所以四边形DMNQ为平行四边形,可得DM∥QN.故DM∥CE,∠DMB即为异面直线CE与BM所成的角(或其补角),利用余弦定理求解即可.
【考点精析】本题主要考查了异面直线及其所成的角和直线与平面垂直的性质的相关知识点,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;垂直于同一个平面的两条直线平行才能正确解答此题.

【题目】某理财公司有两种理财产品A和B.这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立): 产品A产品B(其中p、q>0)
投资结果 | 获利40% | 不赔不赚 | 亏损20% |
概率 |
|
|
|
投资结果 | 获利20% | 不赔不赚 | 亏损10% |
概率 | p |
|
(1)已知甲、乙两人分别选择了产品A和产品B进行投资,如果一年后他们中至少有一人获利的概率大于 ![]() ,求p的取值范围;
,求p的取值范围;
(2)丙要将家中闲置的10万元钱进行投资,以一年后投资收益的期望值为决策依据,在产品A和产品B之中选其一,应选用哪个?