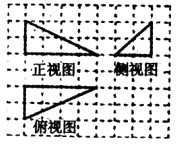
题目内容
【题目】各项均为非负整数的数列{an}同时满足下列条件: ①a1=m(m∈N*);②an≤n﹣1(n≥2);③n是a1+a2+…+an的因数(n≥1).
(Ⅰ)当m=5时,写出数列{an}的前五项;
(Ⅱ)若数列{an}的前三项互不相等,且n≥3时,an为常数,求m的值;
(Ⅲ)求证:对任意正整数m,存在正整数M,使得n≥M时,an为常数.
【答案】解:(Ⅰ) m=5时,数列{an}的前五项分别为:5,1,0,2,2.
(Ⅱ)∵0≤an≤n﹣1,∴0≤a2≤1,0≤a3≤2,
又数列{an}的前3项互不相等,
⑴当a2=0时,
若a3=1,则a3=a4=a5=…=1,
且对n≥3, ![]() 都为整数,∴m=2;
都为整数,∴m=2;
若a3=2,则a3=a4=a5=…=2,
且对n≥3, ![]() 都为整数,∴m=4;
都为整数,∴m=4;
⑵当a2=1时,
若a3=0,则a3=a4=a5=…=0,
且对n≥3, ![]() 都为整数,∴m=﹣1,不符合题意;
都为整数,∴m=﹣1,不符合题意;
若a3=2,则a3=a4=a5=…=2,
且对n≥3, ![]() 都为整数,∴m=3;
都为整数,∴m=3;
综上,m的值为2,3,4.
(Ⅲ)证明:对于n≥1,令Sn=a1+a2+…+an,
则 ![]() .
.
又对每一个n, ![]() 都为正整数,∴
都为正整数,∴ ![]() ,其中“<”至多出现m﹣1个.
,其中“<”至多出现m﹣1个.
故存在正整数M>m,当n>M时,必有 ![]() 成立.
成立.
当 ![]() 时,则
时,则 ![]() .
.
从而 ![]() .
.
由题设知 ![]() ,又
,又 ![]() 及an+1均为整数,
及an+1均为整数,
∴ ![]() =an+1=
=an+1= ![]() ,故
,故 ![]() =常数.
=常数.
从而 ![]() =常数.
=常数.
故存在正整数M,使得n≥M时,an为常数
【解析】(Ⅰ)当m=5时,写出数列{an}的前五项;(Ⅱ)对a2、a3分类取值,再结合各项均为非负整数列式求m的值;(Ⅲ)令Sn=a1+a2+…+an,则 ![]() .进一步推得存在正整数M>m,当n>M时,必有
.进一步推得存在正整数M>m,当n>M时,必有 ![]() 成立.再由
成立.再由 ![]() 成立证明an为常数.
成立证明an为常数.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系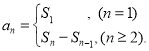 ).
).

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案【题目】某单位附近只有甲,乙两个临时停车场,它们各有50个车位,为了方便市民停车,某互联网停车公司对这两个停车场在工作日某些固定时刻的剩余停车位进行记录,如下表:
时间 | 8点 | 10点 | 12点 | 14点 | 16点 | 18点 |
停车场甲 | 10 | 3 | 12 | 6 | 12 | 17 |
停车场乙 | 13 | 4 | 3 | 2 | 6 | 19 |
如果表中某一时刻停车场剩余停车位数低于总车位数的10%,那么当车主驱车抵达单位附近时,该公司将会向车主发出停车场饱和警报.
(Ⅰ)假设某车主在以上六个时刻抵达单位附近的可能性相同,求他收到甲停车场饱和警报的概率;
(Ⅱ)从这六个时刻中任选一个时刻,求甲停车场比乙停车场剩余车位数少的概率;
(Ⅲ)当停车场乙发出饱和警报时,求停车场甲也发出饱和警报的概率.
【题目】2017年3月27日,一则“清华大学要求从2017级学生开始,游泳达到一定标准才能毕业”的消息在体育界和教育界引起了巨大反响.游泳作为一项重要的求生技能和运动项目受到很多人的喜爱.其实,已有不少高校将游泳列为必修内容.某中学为了解2017届高三学生的性别和喜爱游泳是否有关,对100名高三学生进行了问卷调查,得到如下列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 |
已知在这100人中随机抽取1人,抽到喜欢游泳的学生的概率为 ![]() .
.
(Ⅰ)请将上述列联表补充完整;
(Ⅱ)判断是否有99.9%的把握认为喜欢游泳与性别有关?
附: ![]()
p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |