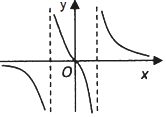
题目内容
【题目】已知曲线C1的参数方程为 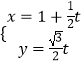 (为参数).在以坐标原点为极点,轴的正半轴为极轴的极坐标系中,曲线C2:
(为参数).在以坐标原点为极点,轴的正半轴为极轴的极坐标系中,曲线C2: ![]() . (Ⅰ)求曲线C1的普通方程和C2的直角坐标方程;
. (Ⅰ)求曲线C1的普通方程和C2的直角坐标方程;
(Ⅱ)若C1与C2相交于A、B两点,设点F(1,0),求 ![]() 的值.
的值.
【答案】解:(I)∵曲线C1的参数方程为  (为参数),
(为参数),
∴ 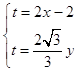 ,∴
,∴ ![]() ,
,
∴曲线C1的普通方程为 ![]() .
.
∵曲线C2: ![]() ,∴3ρ2+ρ2sin2θ=12,
,∴3ρ2+ρ2sin2θ=12,
∴3(x2+y2)+y2=12,∴3x2+4y2=12,
∴C2的直角坐标方程为 ![]() .
.
(Ⅱ)由题意可设,与A、B两点对应的参数分别为t1,t2,
将C1的参数方程代入C2的直角坐标方程 ![]() ,
,
化简整理得,5t2+4t﹣12=0,∴ 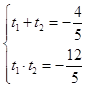 ,
,
∴  ,
,
∵ ![]() ,∴
,∴ 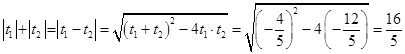 ,
,
∴ 
【解析】(I)曲线C1的参数方程消去参数能求出曲线C1的普通方程;由曲线C2极坐标方程,能求出C2的直角坐标方程.(Ⅱ)由题意可设,与A、B两点对应的参数分别为t1,t2,将C1的参数方程代入C2的直角坐标方程,得:5t2+4t﹣12=0,由此能求出

 名校课堂系列答案
名校课堂系列答案【题目】为调查了解某省属师范大学师范类毕业生参加工作后,从事的工作与教育是否有关的情况,该校随机调查了该校80位性别不同的2016年师范类毕业大学生,得到具体数据如表:
与教育有关 | 与教育无关 | 合计 | |
男 | 30 | 10 | 40 |
女 | 35 | 5 | 40 |
合计 | 65 | 15 | 80 |
(1)能否在犯错误的概率不超过5%的前提下,认为“师范类毕业生从事与教育有关的工作与性别有关”? 参考公式: ![]() (n=a+b+c+d).
(n=a+b+c+d).
附表:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.023 | 6.635 |
(2)求这80位师范类毕业生从事与教育有关工作的频率;
(3)以(2)中的频率作为概率.该校近几年毕业的2000名师范类大学生中随机选取4名,记这4名毕业生从事与教育有关的人数为X,求X的数学期望E(X).
【题目】2017年3月27日,一则“清华大学要求从2017级学生开始,游泳达到一定标准才能毕业”的消息在体育界和教育界引起了巨大反响.游泳作为一项重要的求生技能和运动项目受到很多人的喜爱.其实,已有不少高校将游泳列为必修内容.某中学为了解2017届高三学生的性别和喜爱游泳是否有关,对100名高三学生进行了问卷调查,得到如下列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 |
已知在这100人中随机抽取1人,抽到喜欢游泳的学生的概率为 ![]() .
.
(Ⅰ)请将上述列联表补充完整;
(Ⅱ)判断是否有99.9%的把握认为喜欢游泳与性别有关?
附: ![]()
p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某理财公司有两种理财产品A和B.这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立): 产品A产品B(其中p、q>0)
投资结果 | 获利40% | 不赔不赚 | 亏损20% |
概率 |
|
|
|
投资结果 | 获利20% | 不赔不赚 | 亏损10% |
概率 | p |
|
(1)已知甲、乙两人分别选择了产品A和产品B进行投资,如果一年后他们中至少有一人获利的概率大于 ![]() ,求p的取值范围;
,求p的取值范围;
(2)丙要将家中闲置的10万元钱进行投资,以一年后投资收益的期望值为决策依据,在产品A和产品B之中选其一,应选用哪个?